

Источник: «dwg.ru»
4-го июля вышел новый перечень обязательных национальных стандартов и сводов правил (частей таких стандартов и сводов правил), в результате применения которых на обязательной основе обеспечивается соблюдение требований Федерального закона «Технический регламент о безопасности зданий и сооружений» и о признании утратившими силу некоторых актов Правительства Российской Федерации.
В прошлом году, в США и России, появились два новых нормативных документа по железобетону. В июне вступил в силу СП 63.13330.2018, а в июле, вышел ACI 318-2019. Американский нормативный документ не переиздавался с 2014 года, а с момента появления СП 63.13330.2012 прошло более семи лет и конечно, каждому конструктору, занимающемуся железобетоном, интересно, для чего понадобилось выпускать СП 63.13330.2018. О чем новом удалось узнать авторам. После внимательного прочтения выясняется, что в основных главах не так много новинок, но чувствуется явное тяготение разработчиков к достижениям науки советской эпохи, что не может не радовать, так как добавить в него могли что угодно. Возможно, авторы посчитали, что в существующем СП уже достаточно требований и методик для «классического железобетона» на обычных бетонах и дополнять их или изменять нет причин. Но тогда зачем его переиздавать, не лучше ли было выпустить обновленную версию Пособия к СП 63. В целом, если не учитывать добавление в пункте 5.1 о том, что расчеты по предельным состояниям второй группы следует производить на действие кратковременных и длительных нагрузок, без упоминания о постоянных нагрузках, которые тоже должны входить в основное сочетание, то остальные добавления можно считать более менее удачными. Например, в пункте 5.2.1, помимо необходимости расчета прочности по деформационной модели, добавили возможность расчета по предельным усилиям. Этот метод расчета хорошо себя зарекомендовал в советский период и используется сейчас во многих расчетных программах, поэтому его возвращение должны поприветствовать разработчики расчетных комплексов. Реализация полноценного расчета по нелинейной деформационной модели всей расчетной схемы требует большой переработки расчетных комплексов, а также привлечение соответствующих специалистов и времени, а главное — дополнительных финансовых затрат. В пункте 8.1.23 появилось полезное уточнение: «При статическом расчете конструкции по недеформированной схеме значения Mx и My определяют с учетом влияния прогибов согласно 8.1.2». В пункте 8.1.34 также добавили полезную поправку: «Значения коэффициента фn принимаются равными 1 — для изгибаемых конструкций без предварительного напряжения арматуры». Например, для изгибаемых конструкций, в которых не учитывается продольная сила коэффициент фn тоже теперь можно не учитывать. Пункт 8.1.46 дополнили следующим текстом: «Значение сосредоточенной силы следует принимать за вычетом сил, действующих в пределах основания пирамиды продавливания в противоположном направлении». Это допущение было описано в «Пособие по проектированию фундаментов на естественном основании под колонны зданий и сооружений (к СНиП 2.03.01-84 и СНиП 2.02.01-83)», в пункте 2.8: «Величина продавливающей силы F принимается равной величине продольной силы N, действующей на пирамиду продавливания, за вычетом величины реактивного давления грунта, приложенного к большему основанию пирамиды продавливания (считая до плоскости расположения растянутой арматуры)», и позволяло экономить арматуру в тех случаях, когда расчет на продавливание проходил с небольшим запасом. Этот пункт позволял немного увеличить запас и поперечную арматуру не устанавливать. Впрочем, сейчас в таких случаях принято устанавливать поперечную арматуру конструктивно (в связи с некачественным производством работ и возможными отклонениями толщины плит от проектных значений), поэтому данное уточнение поможет Заказчикам более аргументированно требовать обоснования расходов арматуры. В 10-й главе, в пункте 10.3.2 появилось требование из пункта 5.8 «Пособия к СП 52-101-2003» о необходимости установки конструктивной арматуры в виде сеток при толщине защитного слоя более 50 мм и отношении усилий M/N > 0.3h. Это требование позволяет предотвращать скалывание защитного слоя, поэтому добавление понятно и оправдано. О главе 10 и о конструктивных требованиях хочется упомянуть более подробно в связи с тем, что к этим требованиям часто относятся не так серьезно, как к расчетным, возможно из-за того, что не все понимают их важность, поэтому лишний раз обратить внимание на эти пункты будет полезно.
Почему конструктивные требования нужно обязательно выполнять? Во-первых, формально, глава 10 СП 63 указана в перечне национальных стандартов и сводов правил, в результате применения которых на обязательной основе обеспечивается соблюдение требований Федерального закона «Технический регламент о безопасности зданий и сооружений». Т. е. выполнение требований главы 10, наравне с другими обязательными главами СП 63, является условием, гарантирующим надежность и безопасность здания в течении всего срока службы. Во-вторых, выполнение конструктивных требований прямым и косвенным образом влияет на возможность выполнения расчетных требований, например, позволяет защищать арматуру от атмосферных (и других) воздействий и обеспечивать её совместную работу с бетоном. Чтобы лучше понять логику некоторых конструктивных требований можно вспомнить историю их появления и развития. Конструктивные требования, до появления в том виде, в каком они сейчас в СП, формировались на протяжении более чем 80 лет с момента выпуска ОСТ 90003-38 («Нормы и технические условия проектирования железобетонных конструкций»). Они менялись, дополнялись, сокращались по мере развития строительных технологий, технологий производства бетона, развития методик расчета и накопления данных испытаний. (Немного истории). Первые испытания железобетона, начались сразу после того, как в 1854 году в Англии и в 1867 году во Франции патенты на него получили Уильям Уилкинсон и Жозеф Монье. В 1861 году, во Франции, строитель Франсуа Куанье публикует первую брошюру о десятилетнем опыте применения железобетона под названием «Применение железобетона в строительном искусстве». А в 1884 году, в Германии, профессор механики И. Баушингер и инженер Г. А. Вайс выполнили первые масштабные исследования для изучения особенностей работы железобетонных конструкций. Кстати, Гюстав Вайс первым начал осознанно устанавливать арматуру в растянутую зону бетона. Например, Монье считал, что арматуру лучше устанавливать в середине сечения. Таким образом, конец 19 века стал периодом активного развития железобетона в Европе и США. В начале 20 века, 1903 году, английский инженер Эрнест Лесли Рэнсом, в Сиэтле, заканчивает строительство самого высокого на тот момент 15-ти этажного здания из железобетона. При том, что первые нормы по железобетону в США появились только в 1921 году (в Германии и Швеции в 1904 году, во Франции в 1906 году).

Не смотря на популярность за рубежом, в России, в это время, инженеры скептически относились к железобетону и не верили в его перспективы. В 1891 году выдающийся русский инженер-мостостроитель, ученый, Николай Аполлонович Белелюбский одним из первых осознал преимущества нового материала и начал многочисленные испытания железобетонных конструкций. Накопленные им данные позволили выявить очевидные плюсы железобетона и разрешить его использование в России, а в 1908 — 1911 годах выпустить первые нормативные документы по его использованию и расчету.
После окончания революции, в России, железобетон начали применять очень активно и появилась необходимость в экономии бетона и арматуры, т. е. в более глубоком изучении железобетона. В связи с этим начали создаваться первые научно-исследовательские институты. В результате, в 30-х годах, А. Ф. Лолейт и А. А. Гвоздев (при участии В. И. Мурашева) создают теорию предельного равновесия конструкций и метод расчета железобетонных элементов по стадии разрушения. Первые предложения по расчету железобетона по стадии разрушения сформулировал А. Ф. Лолейт и в 1932 году, на II Всесоюзной конференции по бетону и железобетону, изложил их в своем докладе: «О пересмотре теории железобетона». Однако, в связи с тем, что он в июне 1933 года ушел из жизни, опытные эксперименты, которые проводились под его руководством продолжил А. А. Гвоздев. Гвоздев также был одним из первых кто предложил выполнять расчет железобетона с учетом диаграмм деформирования бетона. (Окончательный переход на эту методику расчета произошел лишь в СНиП 52-01 «Железобетонные и бетонные конструкции»). В это же время В. З. Власов создает свою теорию расчета тонкостенных оболочек. Таким образом первые конструктивные требования к железобетонным конструкциям, в СССР, сформировались в 30-е годы и постепенно дополнялись с выходом обновлений нормативных документов. История развития некоторых из них описана далее.
Процент армирования
Первые требования к минимальному проценту армирования железобетонных конструкций появились в ОСТ 90003-38, в котором появился метод расчета по разрушающим усилиям. В книге Василия Ивановича Мурашова «Расчет железобетонных элементов по стадии разрушения», вышедшей в 1938 г., которая стала пособием к вышедшему ОСТ, о минимальном проценте армирования говорится следующее: «Минимальный процент насыщения сечения арматурой зависит от различных причин: величины усадочных напряжений, конструктивных соображений и т. д. В элементах, в которых часть сечения сжата, а часть растянута, минимальный процент растянутой арматуры должен быть согласно нормам не менее величин, приведенных в табл. 1.
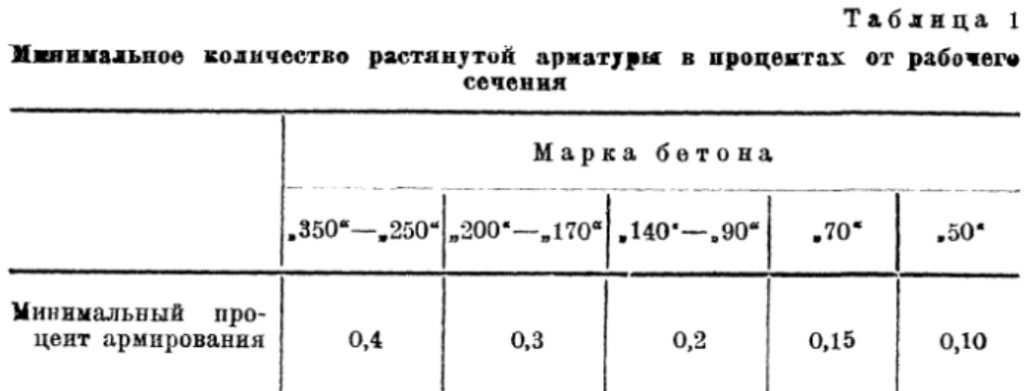
Минимальные проценты армирования определены из условия, чтобы прочность железобетонного сечения была не ниже прочности того же сечения, рассчитанного как бетонное без учета арматуры. Для тавровых сечений минимальный процент армирования относится к площади сечения ребра…».
В вышедшем в 1946 году Н-3-46 («Нормы проектирования железобетонных конструкций (Н-3-46)», в таблице добавили информацию о напряжениях в арматуре, о количестве арматуры было написано следующее: «19. Сечение растянутой арматуры в процентах от площади расчетного сечения бетона для изгибаемых, внецентренно растянутых и внецентренно сжатых элементов, рассчитываемых в предположении, что при разрушении элемента имеет место текучесть арматуры, должно быть не менее указанного в табл. 4.
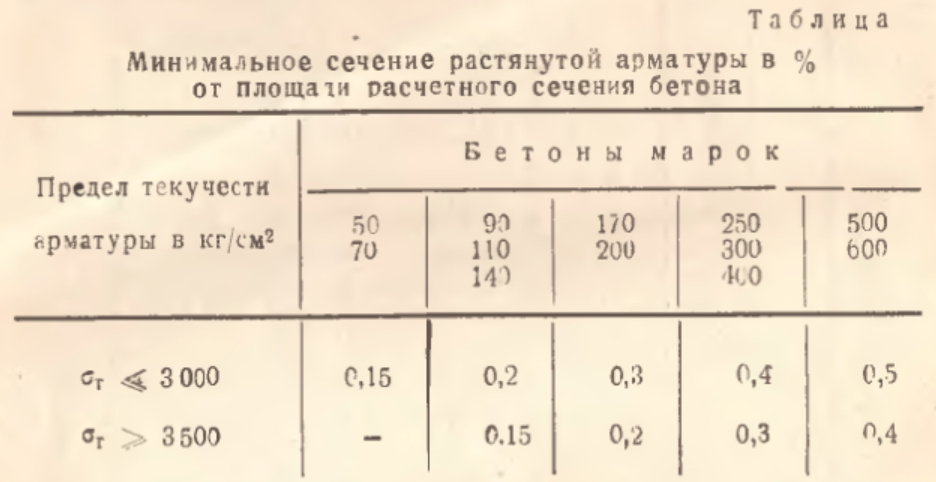
В центрально сжатых элементах, а также внецентренно сжатых, рассчитываемых в предположении, что при их разрушении текучести растянутой арматуры не происходит, сечение продольной арматуры должно быть не менее 0,5% от площади расчетного сечения бетона независимо от его марки».
Про максимальный процент армирования в книге Мурашева написано следующее: «При насыщении сечения колонны продольной арматурой не более 3%, как показали опыты, достаточно обычных хомутов, поставленных через 10-15 диаметров продольной арматуры. Если насыщение продольной арматурой превышает 3%, то для удержания мощных стержней от выпучивания обычных хомутов может оказаться недостаточно. В этом случае требуется взамен обычных хомутов ставить спиральную арматуру или приваренные хомуты. При этом каждый стержень продольной арматуры должен находиться в сгибе хомута. Таким образом для коротких колонн нормы не ограничивают предельный процент продольной арматуры, однако при высоких процентах насыщения требуют усиленного поперечного армирования».
Данное требование есть и в СП 63, в пункте 10.3.14: «Если содержание сжатой продольной арматуры, устанавливаемой у одной из граней элемента, более 1,5%, поперечную арматуру следует устанавливать с шагом не более 10d и не более 300 мм». Однако это требование не относится к случаям, когда арматура установлена не по расчету, а конструктивно с большим диаметром большей площади, чем требуется по расчету, так как при увеличении диаметра арматуры напряжения в ней уменьшаются и устойчивость увеличивается. Также уменьшаются и напряжения в бетоне. Нужно также иметь в виду, что при насыщении арматурой более 3% напряжения в бетоне рассчитываются с учетом вычета площади арматуры.
Максимальный процент армирования СП 63 не ограничивает, что не может не вызывать вопросов, так как в разных нормативных документах требования отличаются. Например, в пункте 8.3.5.1 СП 266 написано следующее: «Наибольший процент армирования колонн продольной жесткой и гибкой арматурой принимают не более 15%. Если при расчете конструкции в ней возникают изгибающие моменты только от случайных эксцентриситетов, то процент армирования принимают не более 25%». А в пункте 5.2.8 СП 430 написано: «…процент армирования в любом сечении (включая участки с нахлесточным соединением арматуры) — не более 10%». Так как СП 63, это обязательный нормативный документ, в нем должен быть указан критерий отнесения конструкции к железобетонной с гибкой или жестко арматурой. Будем надеяться, что со временем такой критерий появится.
…
Учет случайного эксцентриситета при расчете сжатых конструкций (п. 7.1.7, 8.1.7 СП 63.13330.2018)
Требование об учете случайного эксцентриситета при расчете сжатых железобетонных элементов, в советских нормах, впервые появились в СНиП II-21-75. Они подробно описаны в книге А. А. Гвоздева «Новое в проектировании бетонных и железобетонных конструкций» (Москва 1978 г.): «Центральное приложение усилия, вызывающее равномерное по сечению укорочение сжимаемого элемента трудно осуществить даже в лабораторных условиях; для этого приходится прибегать к пробным нагружениям испытуемого образца небольшим усилием по измерениям деформаций на гранях, оценивать эксцентриситет и его направление, разгружать образец и передвигать его в прессе для достижения более равномерной деформации. Такую операцию иногда повторяют несколько раз. Тем более нельзя рассчитывать, что кокой-либо элемент в реальной конструкции будет сжат центрально. Между тем даже небольшой эксцентриситет ощутимо снижает несущую способность сжатого элемента. Причиной возникновения случайного эксцентриситета могут быть: неоднородность свойств бетона по сечению, особенно в случае бетонирования элементов в горизонтальном положении, при значительной высоте сечения и подвижной консистенции бетона; начальная кривизна оси сжатого элемента или ее отклонение от вертикали; неучтенные горизонтальные силы и другие причины. Случайный эксцентриситет принимается… равным большему из трех значений: 1/600 свободной высоты сжатого элемента, 1/30 высоты сечения, 1 см. Эти величины заимствованы из рекомендаций Европейского комитета по бетону (ЕКБ) и Международной федерации преднапряженного железобетона (ФИП) и приняты также в нормах ряда стран. Согласно строительному кодексу Американского института бетона, случайный эксцентриситет принимается равным 1/10 высоты сечения сжатого элемента. В нормах зарубежных стран, учитывающих случайный эксцентриситет, он во всех случаях суммируется с эксцентриситетом, определенным расчетом. В наших… нормах это правило сохранено для статически определимых конструкций. Для статически неопределимых конструкций сделано послабление: если эксцентриситет, определенный из расчета, меньше случайного, то принимается случайный эксцентриситет; если же из расчета определен эксцентриситет, превышающий случайный, то последний не учитывается. Это обосновывается следующими соображениями. Наличие случайного эксцентриситета должно приводить к взаимному смещению концов сжатого стержня. Но в статически неопределимой конструкции такому смещению в той или иной мере препятствует связь этого стержня с другими элементами конструкции, что несколько смягчает влияние случайного эксцентриситета. Смягчение это существенно для сечений, где расчетный эксцентриситет значителен, и ничтожно либо отсутствует вовсе в сечениях, где он велик».

Технология бетонной 3d печати начала развиваться в 90-х годах прошлого века и практически сразу привлекла к себе внимание инвесторов. Очевидным преимуществом данной технологии является скорость их возведения, стоимость возведения, а также отсутствие необходимости выполнения сложных опалубочных работ. Эта технология уже сейчас позволяет возводить небольшие одноэтажные или двухэтажные дома в течении нескольких дней практически любой геометрической формы. Такая скорость строительства особенно востребована после масштабных стихийных бедствий, после которых нужно в короткие сроки возвести большое количество жилья, а также в городах разрушенных в результате военных действий.
В этом направлении, за рубежом, наиболее известны две компании, компания WinSun и компания Contour Crafting. Принципиальное отличие между этими компаниями в том, что WinSun создает типовые дома на своих строительных площадках. После возведения эти дома разрезаются на отдельные блоки, перевозятся на место строительства и там собираются. Компания Contour Crafting создает 3d дома непосредственно на месте строительства, поэтому сроки возведения сокращаются до минимальных и стоимость возведения уменьшается до пяти раз. При всех минусах (отсутствия нормативной базы, отсутствия экспериментальных данных, отсутствия необходимой номенклатуры строительных материалов для данной технологии) это направление строительства является очень перспективным.
В настоящее время одним из самых популярных и востребованных направлений использования бетонных 3d принтеров является возведение малых архитектурных форм. Данная технология позволяет быстро создать малую архитектурную форму любой конфигурации и при этом не требует возведения специальных технологических линий, которые обычно сооружают на заводах ЖБИ.



Совершенствование оборудования печати со временем позволит возводить не только бетонные, но и железобетонные дома и позволит перейти на новый уровень производства строительно монтажных работ, при котором строители будут только устанавливать арматурные (или композитные) сетки, а бетонирование будет происходить автоматизированным способом, с помощью 3d принтеров. Соединение печатающего устройства с крановым оборудованием также позволит возводить дома комбинированной конструкции с бетонными стенами и деревянной кровлей, или бетонным каркасом и панельными стенами (типа каркасно обшивных), что расширит возможности применения данного оборудования для конкретных нужд потребителей и позволит перейти строительной отрасли монолитного домостроения на новый технологический уровень.
Ссылки на другие современные технологии в строительстве:
Расчет трещиностойкости железобетонных конструкций в советских нормах появился благодаря выдающемуся советскому инженеру, ученому, создателю теории трещиностойкости Василию Ивановичу Мурашеву, который занимался исследованиями железобетонных конструкций вместе с автором первых советских норм по железобетону, Гвоздевым А. А. Мурашев был одним из первых, кто обратил внимание на важность ширины раскрытия трещин в железобетонных конструкциях. В своей книге «Трещиностойкость, жесткость и прочность железобетона (основы сопротивления железобетона). Москва 1950 г.» он пишет: «При изучении сопротивления железобетона, помимо расчета прочности и жесткости, приходится рассматривать особую задачу, присущую железобетону, а именно: образование трещин в растянутой зоне железобетонного сечения. На базе исследований советских ученых… разработаны методы расчета прочности железобетонных элементов, в основу которых положены теоретические предпосылки, предложенные А. Ф. Лолейтом. Однако практика строительства и эксплуатации железобетонных конструкций показала, что, кроме расчета прочности, необходима безотлагательная разработка методов расчета появления и раскрытия трещин, а также жесткости железобетонных элементов, т. е. необходима общая теория сопротивления железобетона». В своих исследованиях он опирался на метод расчета еще одного выдающегося советского ученого мирового уровня, внесшего огромный вклад в развитие общей теории железобетона, профессора Артура Фердинандовича Лолейта (г. Орел), который доказал, что: «При процентах армирования, не превышающих определенной предельной величины, разрушение сечения происходит тогда, когда напряжения в арматуре равны пределу текучести, а напряжения в сжатой зоне бетона — пределу прочности бетона при изгибе, причем кривизна эпюры сжатой зоны бетона весьма мало влияет на прочность сечения, а потому можно принять любую из возможных форм эпюры сжатой зоны» и создал в 1932 году новый принцип расчета конструкций по стадии разрушения.
Василий Иванович Мурашев ввел в теорию расчета трещиностойкости учет работы растянутого бетона между трещинами (определил влияние растянутого бетона между трещинами, с учетом влияния сцепления арматуры с бетоном, на уменьшение напряжений в арматуре в этой зоне), а также обратил внимание инженеров на то, что арматуру (из-за её возможной коррозии), при расчете прочности, можно использовать с полным расчетным сопротивлением только при условии контроля ширины раскрытия трещин. Его теория (использование треугольной эпюры в сжатой и прямоугольной в растянутой зонах сечения) также была использована при разработке методов расчета по образованию трещин в нормальном к продольной оси сечении изгибаемых элементов. Его первый, приближенный, метод расчета, основанный на экспериментах с однопролетными балками, плитами и колоннами, вошел в первые нормативные документы по расчету железобетонных конструкций (СССР и других стран) и потом лишь уточнялся с помощью дополнительных эмпирических коэффициентов, которые получали из большого количества экспериментов в этой области. Однако, не смотря на огромное количество экспериментов и научных трудов по этой теме, до сих пор (спустя почти 60 лет после добавления этих требований в первые нормы), нет точной и исчерпывающей методики определения ширины раскрытия нормальных и наклонных трещин в железобетонных конструкциях. Например, современные российские расчетные комплексы, при определении ширины раскрытия трещин в плитах, работающих в двух направлениях, пользуются эмпирическими формулами, основанными на экспериментах однопролетных балок и плит, работающих в одном направлении. При этом разработчики комплексов сами пишут о несовершенстве теории расчета (см. например статью [1]), указанной в нормах. Тем не менее, за прошедшее время, построено огромное количество зданий и сооружений из монолитного железобетона и, в целом, приближенная методика расчета по трещиностойкости, разработанная в середине 30-х годов прошлого века нашим инженерами, подтвердила свою состоятельность не смотря на приближенные методы, которыми они пользовались при её создании.
Краткая история развития формулы расчета.
Указания о необходимости проверки железобетонной конструкции на образование и раскрытие трещин было добавлено в «Нормы и технические условия проектирования бетонных и железобетонных конструкций (НиТУ 123-55)». В этом документе появилось и значение максимально допустимой ширины раскрытия трещин — 0,2 мм. Формула расчета ширины раскрытия трещин ат на уровне центра тяжести наиболее растянутой арматуры в центрально растянутых и изгибаемых элементах прямоугольного сечения, в этом нормативном документе выглядела так:
ат = ψа * (σа / Eа) * lт,
где ψа — коэффициент, учитывающий работу растянутого бетона между трещинами, принимаемый не более 1;
σа — напряжение в растянутой арматуре, равное: при растяжении Nн/Fа; при изгибе Mн/W;
lт — расстояние между трещинами.
В СНиП II-В.1-62 общая формула расчета ширины раскрытия трещин нормальных к продольной оси элемента не изменилась, однако теперь эта формула могла использоваться не только для центрально растянутых и изгибаемых элементов, но и для внецентренно растянутых при e0>0,8h0 и внецентренно сжатых элементов. Для новых видов напряженных состояний были добавлены формулы для расчета коэффициента ψа, напряжений в арматуре σа и расстояния между трещинами lт. В этот нормативный документ также добавили указания для расчета ширины раскрытия трещин при многократно повторяющейся нагрузке и для предварительно напряженных элементов.
Многочисленные эксперименты, проведенные после выхода СНиП II-В.1-62 выявили большой разброс ширины раскрытия трещин, зависящий от многих факторов. В вышедшем через некоторое время СНиП-е II-21-75, вместо используемой ранее, была добавлена новая эмпирическая формула, которая учитывала такие факторы как: вид напряженного состояния элемента (изгиб, сжатие или растяжение), длительность действия нагрузки, вид продольной арматуры и растягивающее напряжение в ней, коэффициент армирования, отнесенный к прямоугольной части сечения и диаметр арматуры. Кроме того, приведены дополнительные коэффициенты, используемые для определения ширины раскрытия трещин при расположении арматуры в несколько рядов по высоте сечения. Расстояние между трещинами, а также коэффициент, учитывающий работу растянутого бетона между трещинами, которые учитывались ранее в явном виде стали учитываться косвенным образом через другие коэффициенты. Также для 2-ой категории трещиностойкости был добавлен расчет по закрытию нормальных и наклонных трещин (сейчас из обязательных норм его убрали, из-за сложности и зависимости от множества неподтвержденных пока факторов).
Формула для определения средней ширины раскрытия трещин, нормальных к продольной оси элемента, на уровне центра тяжести наиболее растянутой арматуры, по СНиП II-21-75:
ат = k*kc*сд*η*(σа/Eа)*20*(3,5-100*μ)*d^0.3
где k — коэффициент, учитывающий возрастание изменчивости ширины раскрытия трещин при растяжении, в отличии от изгиба или сжатия. При изгибе и сжатии он равен — 1, при растяжении — 1,2;
kc — коэффициент, учитывающий влияние толщины защитного слоя бетона со стороны арматуры. На основании опытов было установлено, что с увеличением толщины защитного слоя бетона в плоскости действия момента происходит, во-первых, увеличение расстояния между трещинами, а следовательно, и увеличения их ширины раскрытия на уровне центра тяжести арматуры, и, во-вторых, существенный рост ширины раскрытия трещин на растянутой грани элемента;
cд — коэффициент, учитывающий длительность действия нагрузки и принимаемый равным: при кратковременном действии нагрузки — 1; при длительном действии нагрузки, а также при действии многократно повторяющейся нагрузки (для конструкций, подлежащих расчету на выносливость) — 1,5. Было принято среднее значение из полученных в экспериментах (1,2…1,8);
η — коэффициент, зависящий от вида продольной растянутой арматуры. По результатам многочисленных экспериментов было установлено, что применение арматуры периадического профиля позволяет уменьшить ширину раскрытия трещин в 1,2…1,5 раза по сравнению с гладкой арматурой;
σа — напряжение в стержнях крайнего ряда растянутой арматуры;
μ — коэффициент армирования сечения, принимаемый равным отношению площади растянутой арматуры к полезной площади сечения бетона без учета сжатых свесов полок (μ = Fа/bh0) , но не более 0,02;
d — диаметр растянутой арматуры в мм.
Пройдет еще 13 лет прежде чем авторы норм напишут: «Ни в нашей стране, ни за рубежом еще не сложилось единого мнения о теоретических предпосылках к расчету ширины раскрытия нормальных трещин и о значимости тех основных параметров, которые должны быть введены в расчет». В вышедшем в это время
Пройдет еще 15 лет и авторы норм опять вернутся к формуле Мурашева, лишь дополнив её коэффициентами, полученными после 50 лет проведения множества экспериментов. В пояснениях к новой редакции норм они напишут: «В Сводах правил к новому
ат = φ1 * φ2 * φ3 * ψs * (σs / Es) * ls,
где φ1 — коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным;
1 — при непродолжительном действии нагрузки;
1, 4 — при продолжительном действии нагрузки (в прошлых нормах был 1,5);
φ2 — коэффициент, учитывающий профиль продольной арматуры и принимаемый равным:
0,5 — для арматуры периодического профиля (классов А300, А400, А500, В500), раньше был 1;
0,8 — для гладкой арматуры (класса А240), раньше был 1,3;
φ3 — коэффициент, учитывающий характер нагружения и принимаемый равным:
1 — для изгибаемых и внецентренно сжатых элементов (не изменился);
1,2 — для растянутых элементов (остался без изменений)…
σs — напряжение в стержнях крайнего ряда растянутой арматуры. Определение напряжения в арматуре производят на основе не
линейной деформационной модели при двухлинейной диаграмме для сжатого бетона, учитывая непродолжительность действия нагрузок и нормативное сопротивление бетона сжатию При этом сопротивление бетона растянутой зоны не учитывается.



Рис.1. Василий Иванович Мурашов — один из выдающихся представителей российских ученых ХХ века, предложил модель деформирования железобетона с трещинами и разработал методы расчета железобетонных элементов по образованию и раскрытию трещин, по деформациям, что учитывает фактическую работу железобетона в стадии эксплуатации. Артур Фердинандович Лолей — выдающийся ученый, первый основоположник развития теории железобетона в России (в 30-40 годах прошлого столетия). Активный участник создания первого нормативного документа в области железобетона, технических условий и норм проектирования и возведения железобетонных и бетонных конструкций и сооружений, изданных в 1931 г. Алексей Алексеевич Гвоздев — разработчик метода расчёта по предельным состояниям и создатель теории расчёта статически неопределимых линейных и плоскостных железобетонных конструкций методом предельного равновесия. (Источник: «http://www.cstroy.ru/about/school/432/»)
Ссылки по теме статьи:
Капительные стыки колонн с плитами перекрытий часто применяют при проектировании нежилых зданий с пролетами более 6 м, а также при больших нагрузках на плиты (например, в подземных и надземных паркингах, торгово-офисных, складских зданиях, а также в различных промышленных сооружениях). Но не смотря на частое использование при проектировании, в наших обязательных нормативных документах нет требований по конструированию и расчету капителей, как отдельного конструктивного элемента. Например, СП 63.13330 (который является обязательным) относит капители к специфическим конструкциям: «Настоящий свод правил не содержит требования по проектированию специфических конструкций (пустотные плиты, конструкции с подрезками, капители и т.п.)«. Так как в терминах и определениях данного нормативного документа авторы не указали, что считать конструкциями с подрезками, и что «капителями и т.п.», остается только предполагать, что речь идет о классических капителях (т.е. утолщениях верхней части колонн), а подрезки — это местное изменение сечения в плите или балке с широкого на более узкое. При отсутствии определений, например, «подрезкой» или конструкцией подобной капители можно также считать короткие консоли колонн, расчет которых приводится в приложении Ж СП 63. Такая путаница получается из-за того, что только небольшая часть нормативных документов по железобетонным конструкциям стала обязательной и многие очевидные для авторов норм понятия приходится уточнять для правильного понимания требований этих документов.
Известно, что капители стали применять в качестве дополнительного конструктивного элемента после создания железобетона, до этого капитель была лишь архитектурным элементом оформления верхней части колонны, т. е. декоративным элементом оформления колонны. С появлением железобетонных конструкций и железобетонных перекрытий их стали использовать для уменьшения пролета плиты, распределения сконцентрированных надколонных моментов, повышения общей жесткости соединения плиты с колонной и уменьшения горизонтальные смещений плит, уменьшения расчетной длины колонн, повышения несущей способности перекрытий на продавливание и уменьшения их прогибов. Со временем их стали применять в зданиях, рассчитываемых на сейсмические воздействия, а также в зданиях рассчитываемых на прогрессирующее обрушение, так как их наличие повышало надежность таких зданий. Появилась потребность и в расчете самих капителей. В России упоминания о капителях при проектировании конструкций начали появляться в начале прошлого века. В частности, при проектировании монолитных перекрытий с капителями. На сегодняшний день об особенностях проектирования капителей написано в нормативных документах разных стран, но в российских обязательных нормах по железобетону требований к их расчету проектированию пока нет.
Чтобы разобраться, является ли конструкция капителью или это утолщение плиты с «подрезкой» в обратную сторону, стоит изучить требования к капителям в зарубежных нормативных документах, а также в технической литературе у нас.
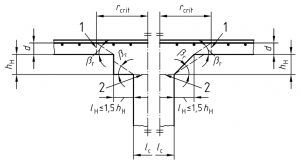
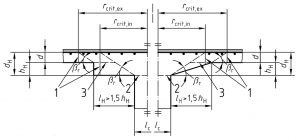
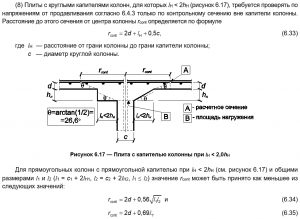
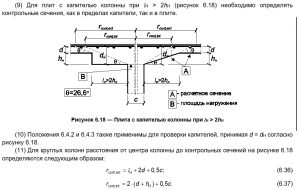
По рекомендациям, описанным в «НАУЧНО-ТЕХНИЧЕСКИЙ ОТЧЕТ по теме: Разработка методики расчета и конструирования монолитных железобетонных безбалочных перекрытий, фундаментных плит и ростверков на продавливание», авторами которого являются и авторы СП 63, проверку прямоугольной капители на продавливание следует проводить при ее вылете за грань колонны более чем в полтора раза превышающем толщину. При меньшем вылете продавливание проверяют в плите за гранью капители. То есть, авторы считают, что при вылете менее 1,5 высоты утолщение можно считать классической капителью (утолщением колонны).
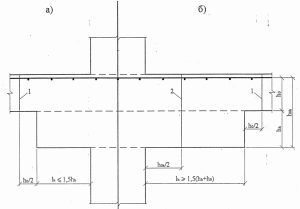
В зарубежной (а также в советской) литературе и нормативных документах используется понятие эффективной ширины оголовка колонны (расчетной ширины капители). Эта ширина ограничивается линиями идущими под углом 45 градусов от центральной оси колонны до нижней поверхности плиты и не зависит от реальной ширины верхней части капители, т.е. если угол наклона более 45 градусов, эффективная ширина все равно принимается не более ширины, ограниченной конусом с гранями, идущими под 45 градусов от оси колонны к плите. Это предположение, в частности, подтверждается экспериментально и аналитически в статье «Experimental and numerical analysis of reinforced concrete mushroom slabs. A. F. Lima Neto; M. P. Ferreira; D. R. C. Oliveira; G. S. S. A. Melo». Со статьей можно ознакомиться по ссылке: http://www.scielo.br/scielo.php?pid=S1983-41952013000200007&script=sci_arttext&tlng=en.
При небольших углах наклона граней капители, теоретически, она может работать и на изгиб (например, при отношении вылета капители к высоте 1/10 и менее), но классическая капитель с углом наклона граней 45 градусов, работает на сжатие по наклонной сжатой бетонной полосе и изгибаемым элементом не является. Её расчет аналогичен расчету короткой консоли, входящей в состав жесткого (рамного) узла, указанного в приложении «Ж» СП 63.
На рисунке 3 показан пример армирования классической, капители из книги «Manual for detailing reinforced concrete structures to EC2. Jose Calavera. 2012»:

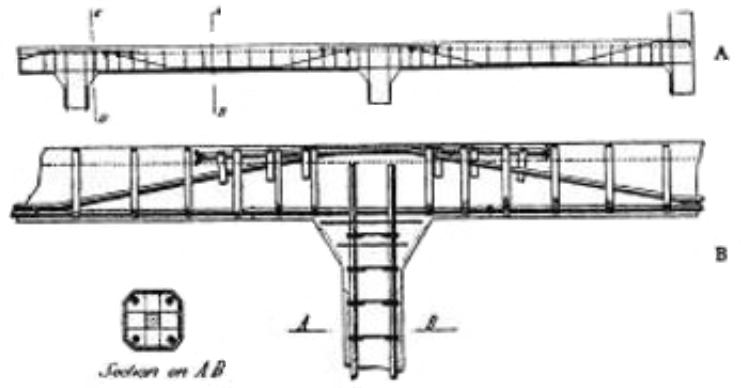

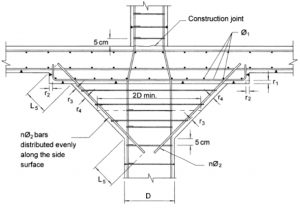





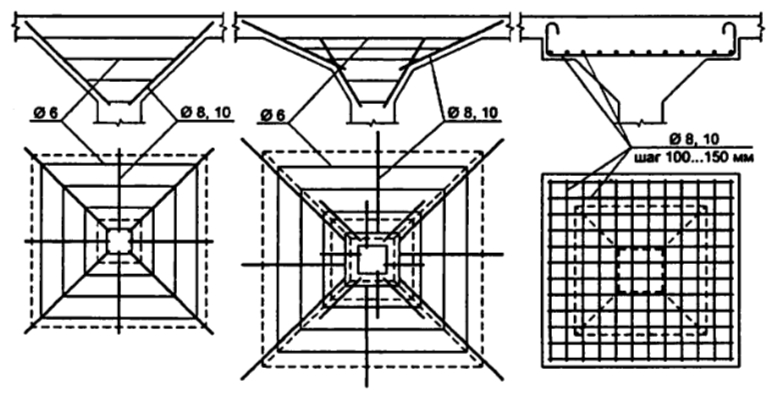










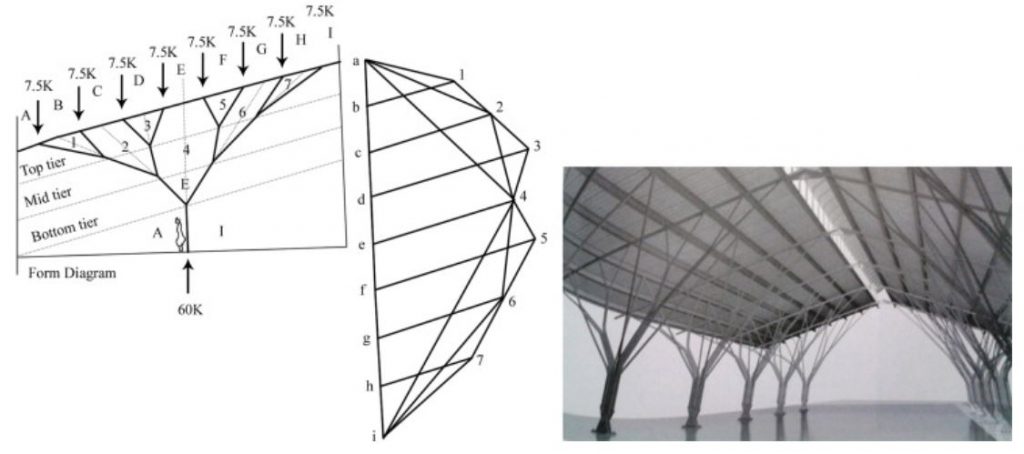


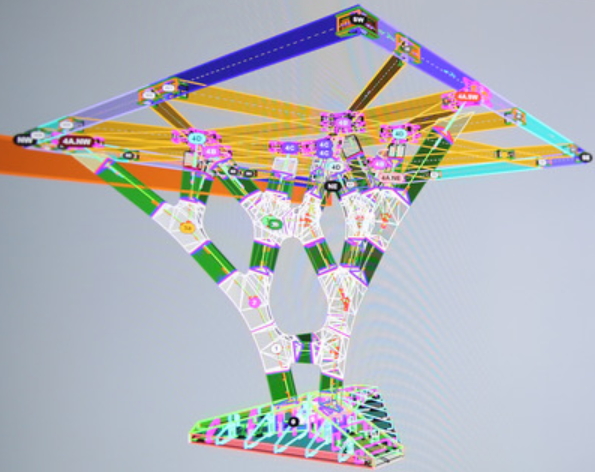

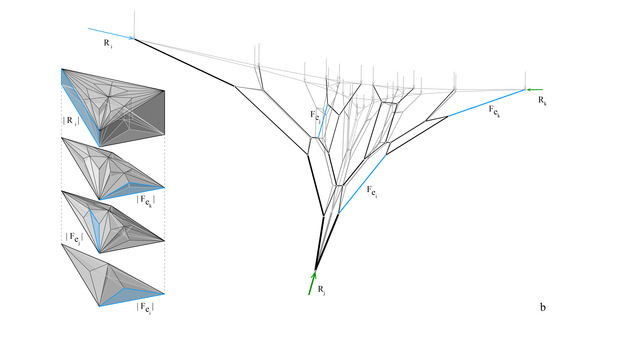
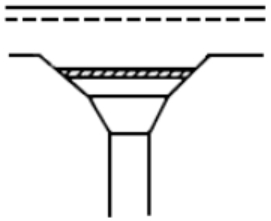
Данная капитель является классической конусообразной капителью колонны, которая армируется наклонными стержнями, которые анкеруются снизу — в колонну, а сверху — в плиту капители. Наклонные стержни охватываются, как обручами, хомутами капители. Кроме этого, внутри капители показаны хомуты колонны, возможно конструктивно (для фиксации вертикальной арматуры). В верхней части капители показана капительная плита. Эту плиту добавляют при больших нагрузках для большего уменьшения пролета и увеличения контура продавливания в вышележащей плите.
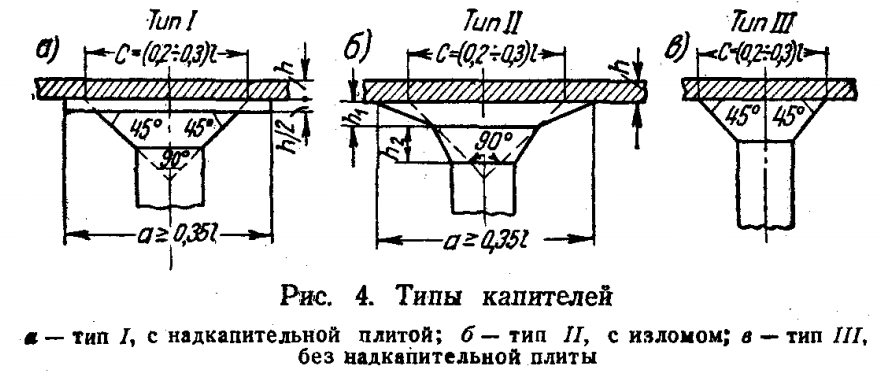
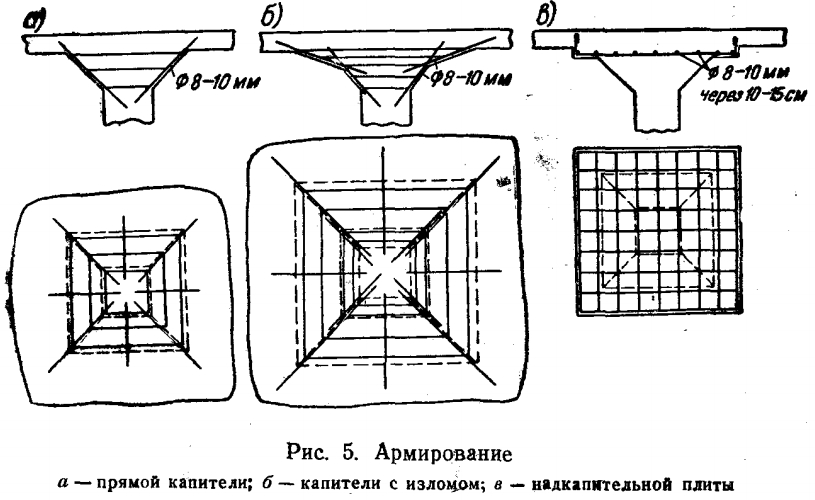
В Советском Союзе капители применяли часто, так как они позволяли экономить арматуру, которой, в те времена не хватало. О капителях, к примеру, написано в книге Штаермана и Ивянского «Безбалочные перекрытия. Москва 1953 г.». Фрагмент из книги: «Размеры капителей должны быть обоснованы и каждый раз проверены расчетом плиты на главные растягивающие напряжения по периметру в местах перелома капителей. При средних величинах нагрузок наиболее целесообразными и экономичными являются размеры капителей, равные 0,35 пролета при расчетной ширине капители С, равной примерно 0,22l. Расчетная ширина капители С должна быть во всех случаях не меньше 0,2l, а верхние наружные размеры капители при капителях I и II — не менее 0,35 величины соответствующего пролета l и при капителях типа III — не менее 0,2l. Армирование капители в огромном большинстве случаев по расчету не требуется, так как сечение ее настолько велико, что растягивающие усилия у наружных граней капители не возникают, а сжимающие усилия всегда меньше допускаемых. Поэтому армирование капителей производится только по конструктивным соображениям для обеспечения лучшей связи ее с колонной и плитой. Прямые капители (без изломов) армируются обычно прямыми стержнями диаметром 8-10 мм, поставленными по углам и по середине сторон и стянутыми по высоте 3-4 хомутами диаметром 6 мм (рис. 5,а). Капители с изломом армируются так же, как прямые капители (рис. 5,б), полукапители пристенных колонн армируются так же, как и средние капители. В капителях с надкапительной плитой капитель армируется, как прямая капитель, а в надкапительной плите, в которой возникают только сжимающие усилия, расчетной арматуры не требуется. Она армируется только по конструктивным соображениям сеткой из стержней диаметром 8-10 мм через 10-15 см с концами, отогнутыми вверх под прямым углом (рис. 5,в)».
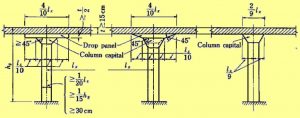
Некоторую информацию о расчете монолитных капителей можно также найти в «Руководство по расчету статически неопределимых железобетонных конструкций. Москва 1975 г». Например, в пункте 4.8 этого документа написано о расчете на продавливание капители: «Капители рассчитываются на продавливание в наиболее слабых местах, например там, где очертание образует входящие узлы… При расчете на продавливание капителей или полукапителей, а также плиты по периметру капителей и полукапителей величина силы Р принимается равной сумме сил, передающихся через перекрытие на рассматриваемую колонну, за вычетом нагрузок, приложенных к верхнему основанию пирамиды продавливания».
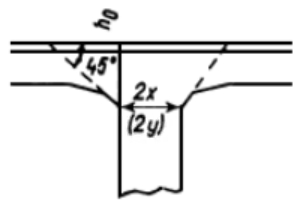
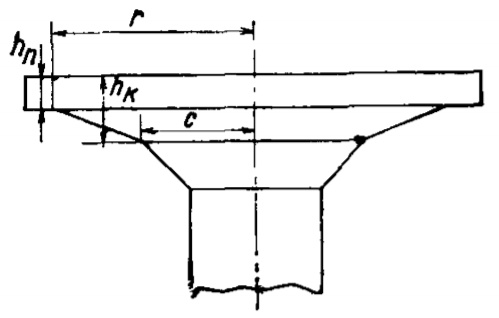
В пункте 4.11 этого Руководства также даны рекомендуемые параметры ломаных капителей: «При применении квадратных или прямоугольных капителей ломаного очертания рекомендуется принимать величину Сх / lx и Cy / ly — пределах от 0,08 до 0,12; отношение высоты hk капители в месте перелома ее очертания к толщине плиты hп в пределах от hk / hп = 2 до hк / hп = 2,5″.
Классические капители с углом наклона граней 45 градусов хороши тем, что их не нужно проверять на продавливание, не нужно армировать по расчету (только конструктивно), они повышают жесткость стыка плиты с колонной и уменьшают прогибы плит. Однако, их главным минусом являются большие габариты, из-за которых возникают сложности с проводкой коммуникаций и планировкой помещений.
При уменьшении высоты капителей и увеличении угла наклона их граней в капителях возникают проблемы с продавливанием и в них устанавливают не горизонтальные, а вертикальные хомуты (или каркасы). Такие капители можно отнести к утолщению плиты.
Ниже приведены схемы определения расчетных сечений в капительных стыках по зарубежным нормам.
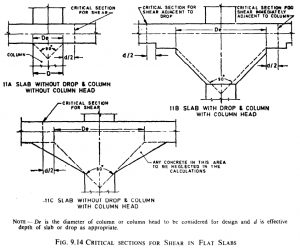
Расчет отдельно стоящих фундаментов с банкетками под железобетонные и стальные колонны на продавливание и на поперечную силу, также описан в главе 2 «Пособия по проектированию фундаментов на естественном основании под колонны зданий и сооружений (к
О конструировании и расчете капителей также говорится в «Руководство по проектированию железобетонных конструкций с безбалочными перекрытиями. Москва Стройиздат 1979».
В некоторых зарубежных нормах можно найти запрет на бетонирование капителей отдельно от основной плиты перекрытия, поэтому данное требование также нужно иметь в виду при проектировании. При необходимости устройства холодных швов бетонирования в местах соединения капители (или банкетки) с основной плитой, данный стык необходимо проверить на сдвиг контактного шва по формуле 5.26-5.32 П 1-98 к СНиП 2.03.01-84*.
В нашей литературе можно встретить также исследования надкапительных стыков. Например, в диссертации «РАЗРАБОТКА И ИССЛЕДОВАНИЕ КАПИТЕЛЬНЫХ УЗЛОВ СОПРЯЖЕНИЯ КОЛОНН С ПЕРЕКРЫТИЯМИ В БЕЗРИГЕЛЬНЫХ КАРКАСАХ МНОГОЭТАЖНЫХ ЗДАНИЙ», автор проводит сравнительное экспериментально-аналитическое исследование «надкапительных» стыков и дает рекомендации по их расчету и конструированию. Основные выводы диссертации:
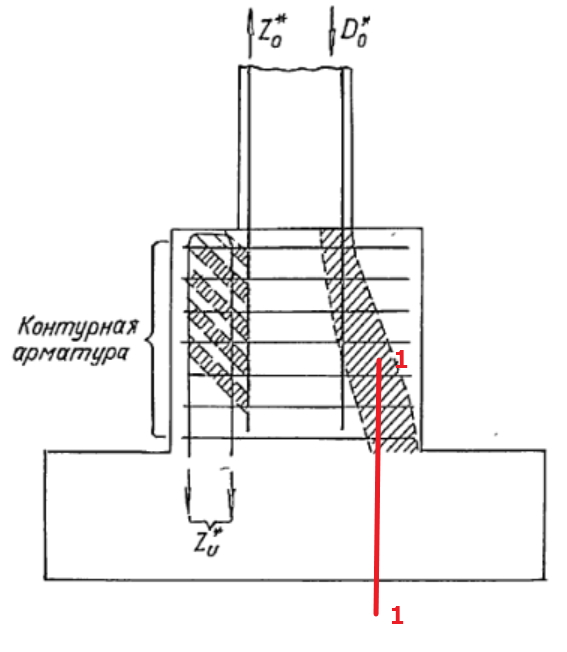
«Определение несущей способности перекрытия с капителями на продавливание при одновременном действии сосредоточенной силы и изгибающего момента производится по двум сечениям возможного образования трещин:
— в первом случае наклонная трещина пирамиды продавливания образуется на стыке капители и плиты, и следует до нижней поверхности перекрытия, пересекая наклонную арматуру (сеч. І-І, рис. 2);
— во втором случае наклонная трещина образуется на верхней по-верхности перекрытия, и следует под углом 45 град. к нижней поверхности плиты к месту начала отгибов наклонной арматуры (сеч. II-II, рис. 2).
1. Расчет по сечению І-І производят из условия:
где F — сосредоточенная сила от внешней нагрузки;
М — изгибающий момент от внешней нагрузки, учитываемый при расчете на продавливание;
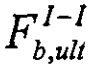
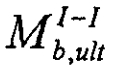
и — предельные сосредоточенная сила и изгибающий момент, воспринимаемые бетоном по сечению І-І;
Fsw,ult и Msw,uit — предельные сосредоточенная сила и изгибающий момент, воспринимаемые наклонной арматурой.
— усилие, воспринимаемое бетоном по сечению І-І, определяется по формуле:
где Rbt — расчетное сопротивление бетона осевому растяжению;
— площадь расчетного сечения І-І, расположенного на расстоянии 0,5h0 от грани колонны при h > с или на расстоянии 0,5(d+h0) при h < с (рис. 2).
— предельный изгибающий момент, воспринимаемый бетоном по сечению І-І, определяют по формуле:
— момент сопротивления расчетного контура поперечного сечения І-І.
Усилие Fsw,ult, воспринимаемое наклонной арматурой, определяется по формуле:
где Rswi, Aswi, — соответственно, расчетное сопротивление растяжению, площадь и угол наклона к горизонтали каждого наклонного арматурного стержня.
2. Расчет по сечению ІІ-ІІ производят из условия:
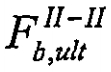
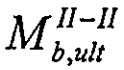
и — предельные сосредоточенная сила и изгибающий момент, воспринимаемые бетоном по сечению ІІ-ІІ.
В результате исследований установлено, что наличие капителей приводит к:
— повышению трещиностойкости и уменьшению прогибов перекрытия на 14 — 22%;
— снижению главных напряжений в опорных зонах перекрытий в 1,5 раза;
— повышению несущей способности стыков на продавливание
на 9 — 42%. Выявлено, что на продавливание наибольшее влияние оказывает армирование капители наклонной арматурой;
— уменьшению изгибающих моментов на опорах на 28 — 34%
и в пролетах — на 7 — 11%, а также уменьшению количества верхней
продольной арматуры на 29 — 36% и нижней продольной арматуры на 6 — 9%;
— снижению горизонтальных деформаций здания до 19%.
3. Проведенные экспериментальные исследования стыков, изготовленных в натуральную величину, показали, что применение капителей приводит к:
— повышению жесткости и трещиностойкости стыковых со
единений перекрытий с колоннами. Причем, наибольшей жесткостью обладает стык с капителью в форме цилиндра. Прогибы плит с капителями до 46% меньше прогибов плиты бескапительного стыка;
— снижению напряжений в продольной арматуре плит на 10 — 20%. Деформации в бетоне снижаются в 2 раза;
повышению несущей способности стыковых соединений на
продавливание на 20 — 50%, в зависимости от формы и размера
капителей, а также их армирования;
5. Технико-экономический анализ показал, что применение капителей приводит к снижению стоимости строительно-монтажных работ по устройству перекрытий на 10% в сравнении с бескапительными перекрытиями. Снижение стоимости устройства перекрытий происходит вследствие уменьшения расхода арматуры на 25%» .
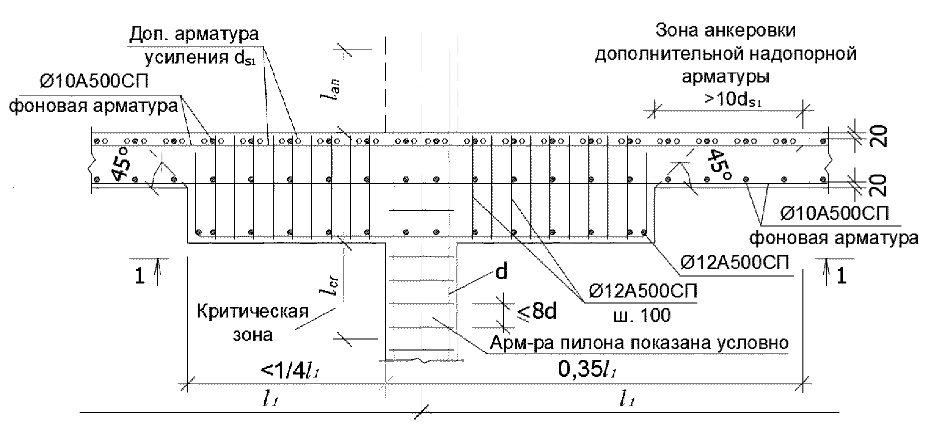
В статье «ОПЫТ ПРОЕКТИРОВАНИЯ И ИСПЫТАНИЙ УСИЛЕННЫХ УЗЛОВ ОПИРАНИЯ МОНОЛИТНЫХ ЖЕЛЕЗОБЕТОННЫХ ПЕРЕКРЫТИЙ НА КОЛОННЫ» авторами проведен численно-экспериментальный анализ «надкапители», и предложен вариант по усилению перекрытия «надкапителью» следующего вида:
В конце статьи, хочется обратить внимание на то, что классическую капитель, которая не требует никаких специальных расчетов и армируется конструктивно, авторы СП 63 отнесли к специфическим конструкциям и не внесли в данный нормативный документ. Из-за большой популярности этого конструктивного элемента, хотелось бы, чтобы авторы наших обязательных норм добавили определение капители и указали параметры, по которым капитель можно считать классической, а также дали рекомендации по её конструктивному армированию.
Ссылки:
Конструированию монолитных железобетонных стен в наших нормативных документах (в отличии от зарубежных) уделено совсем немного внимания. В большей степени это связано с тем, что массовое монолитное строительство появилось относительно недавно, а в советском союзе большая часть массово строящихся зданий были панельными и малоэтажными. Кроме того, расцвет монолитного строительства совпал с развалом в научно-исследовательских институтах, что не могло способствовать появлению передовых идей в области монолитного строительства. В панельных зданиях типовых серий со стеновой конструктивной системой вертикальные усилия в стенах небольшие, а панели соединяются шарнирно с помощью закладных деталей, т. е. моменты с плит, практически, не передаются на стены, что делает возможным армировать панели конструктивно, сетками, с некоторым учащением возле проемов и торцов стен, но особых требований к расположению арматуры в них не предъявляется.
В главном, на сегодняшний день, нормативном документе по железобетонным конструкциям, — СП 63.13330 (который был частично гармонизирован с еврокодом) содержится лишь несколько требований к расположению продольной и поперечной арматуры в стенах, описанных, в основном, общими фразами. Для продольной арматуры, в пунктах 10.4.3 и 10.4.7, главный акцент сделан на том, что вертикальная и горизонтальная арматура в стене должна устанавливаться симметрично у боковых сторон, и в соответствии с действующими в ней усилиями. Хочется обратить внимание на формулировку пункта 10.4.7: «Количество вертикальной и горизонтальной арматуры в стене следует устанавливать…». Авторы норм в одном предложении дважды (но по-разному) описали одно и тоже требование: количество вертикальной и горизонтальной арматуры в стене определяется в соответствии с действующими в ней усилиями, вертикальная и горизонтальная арматура в стене должна устанавливаться в соответствии с действующими в ней усилиями. Т. е. речь идет о том, что, если в какой-то части стены усилия больше, то из этого логически следует, что и арматуры, на этом участке стены, должно быть установлено больше. Правда, в следующем предложении пункта 10.4.7 говорится о необходимости равномерного армирования по площади стены, но с конструктивным учащением арматуры на торцах и возле проемов, т. е. даже если усилия на этих участках не увеличиваются.
Расстояние между соседними стержнями вертикальной арматуры стен не должно превышать двух толщин стены (или 400 мм) и не должно быть менее 50 мм в свету. Поперечная арматура в виде П-образных или замкнутых хомутов устанавливается на торцевых участках стен для обеспечения анкеровки продольной арматуры, а шаг поперечных стержней подбирается в соответствии с действующими в стене усилиями таким образом, чтобы избежать выпучивания продольной арматуры.
В зарубежных нормативных документах, в частности в «Code of Practice for Structural Use of Concrete 2013» (нормах КНР, Гонконг), требования к продольному армированию стен расписаны более развернуто. Учащение вертикальной арматуры у торцов стен — это не конструктивное требование (как в СП 63.13330), а требование, напрямую зависящее от действующих в стене усилий, и проиллюстрировано в виде примеров армирования, а не описано общими фразами. Скорее всего, выводы и иллюстрации были сделаны на основании проведения масштабных экспериментов и анализа большого количества экспериментальных данных.
Требования к раскладке арматуры описаны в главе 9.9.3 «Стены».
П. 9.9.3.2 Участки стен с увеличенным армированием.
(а) Усиленный участок стены — Тип 1.
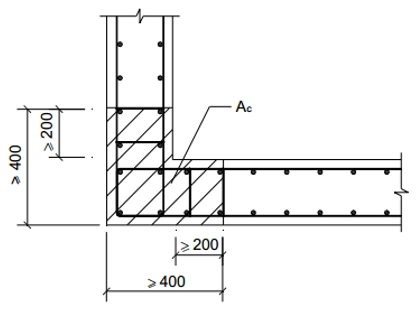
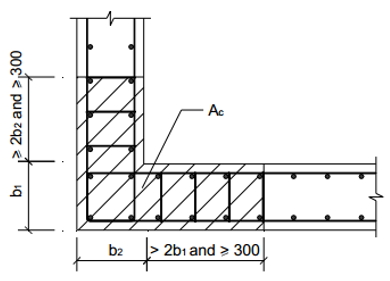
Тип 1 — это закрашенный участок стены, показанный на рисунках 1 и 2, который должен армироваться в соответствии со следующими требованиями:
(i) площадь арматуры, установленной в пределах заштрихованного участка стены должна быть не менее 0,6% его площади (площади заштрихованного бетона);
(ii) диаметр устанавливаемой арматуры должен быть не менее 12 мм и количество не менее 6 шт.;
(iii) каждый из устанавливаемых стержней должен быть связан хомутами (поперечными стержнями) диаметром не менее 10 мм, с шагом по высоте не более 250 мм.
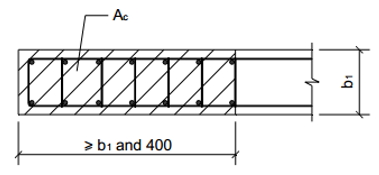
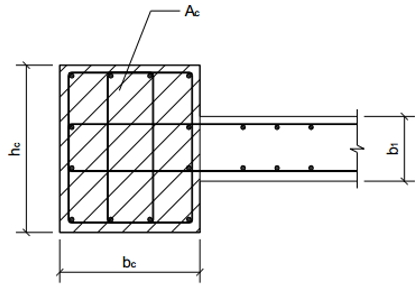
(b) Тип 2 — несвободный усиленный участок стены.
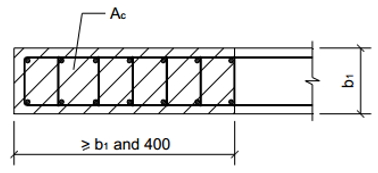
Тип 2 — это несвободный, закрашенный участок стены, показанный на рисунках 3 и 4, который должен армироваться в соответствии со следующими требованиями:
(i) площадь арматуры, установленной в пределах заштрихованного участка стены должна быть не менее 0,8% его площади (площади заштрихованного бетона);
(ii) диаметр устанавливаемой арматуры должен быть не менее 16 мм и количество не менее 6 шт.;
(iii) каждый из устанавливаемых стержней должен быть связан хомутами (поперечными стержнями) диаметром не менее 10 мм, с шагом по высоте не более 200 мм.
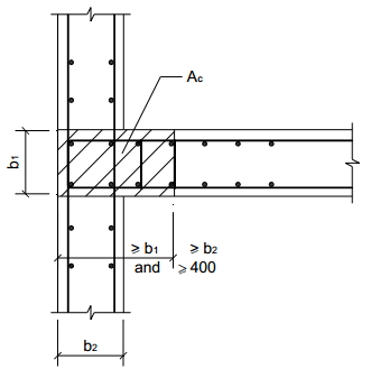
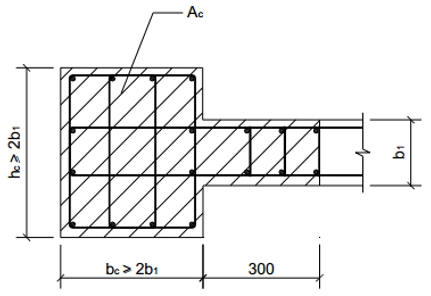
(c) Тип 3 — усиленный участок стены.
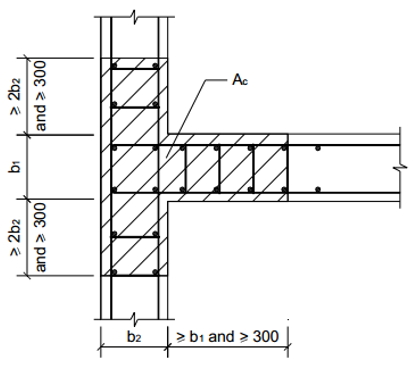
Тип 3 — это закрашенный участок стены, показанный на рисунках 5-8, который должен армироваться в соответствии со следующими требованиями:
(i) площадь арматуры, установленной в пределах заштрихованного участка стены должна быть не менее 1% его площади (площади заштрихованного бетона);
(ii) диаметр устанавливаемой арматуры должен быть не менее 16 мм и количество не менее 6 шт.;
(iii) каждый из устанавливаемых стержней должен быть связан хомутами (поперечными стержнями) диаметром не менее 10 мм, с шагом по высоте не более 150 мм.
9.9.3.3 Определение критической силы Ncr.
Значение критической силы Ncr осевого сжатия стен определяется по формуле:
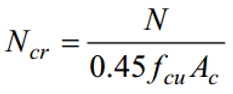
где N = 1.4Gk + 1.6Qk;
fcu — прочность бетона;
Ac — площадь бетона;
Ncr не должно превышать 0,75.
9.9.3.4 Стены в которых 0 < Ncr < 0,38 в пределах критической зоны.
Стена должна быть усилена следующим образом:
а) критическая зона стены должна быть усилена с помощью усиленного армирования Типа 2;
b) все вышележащие этажи должны быть усилены с помощью усиленного армирования Типа 1.
9.9.3.5 Стены в которых 0,38 < Ncr < 0,75 в пределах критической зоны.
Стена должна быть усилена следующим образом:
а) критическая зона стены рассматриваемого этажа и этажа выше должна быть усилена с помощью усиленного армирования Типа 3;
b) все остальные этажи должны быть усилены с помощью усиленного армирования Типа 1.
Из приведенных выше требований двух нормативных документов можно сделать вывод о важности армирования краевых участков стен. Причем, если в СП 63.13330 написано лишь о том, что необходимо устанавливать арматуру в зависимости от действующих усилий, то в Code of Practice for Structural Use of Concrete 2013 расписано, как и какую арматуру нужно устанавливать при различных значениях усилий; а также сделан акцент на том, что краевые участки стен работают, как монолитно соединенные со стеной колонны.
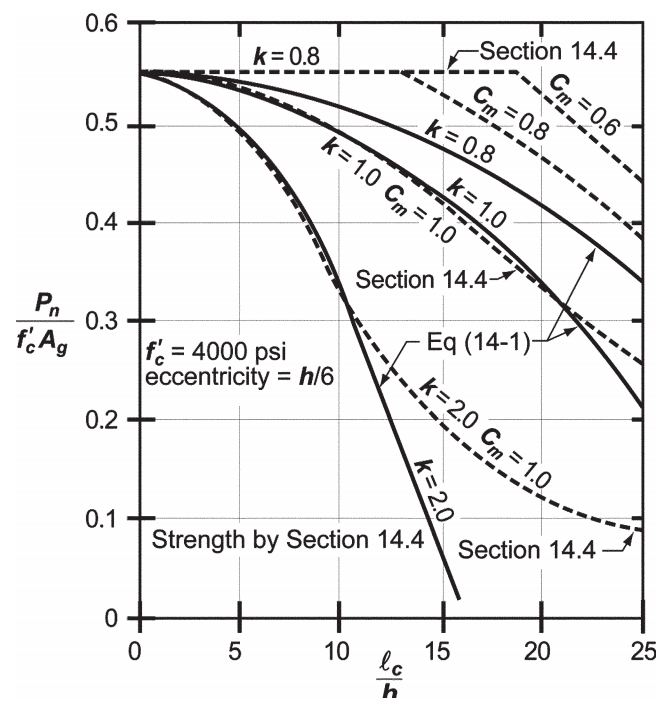
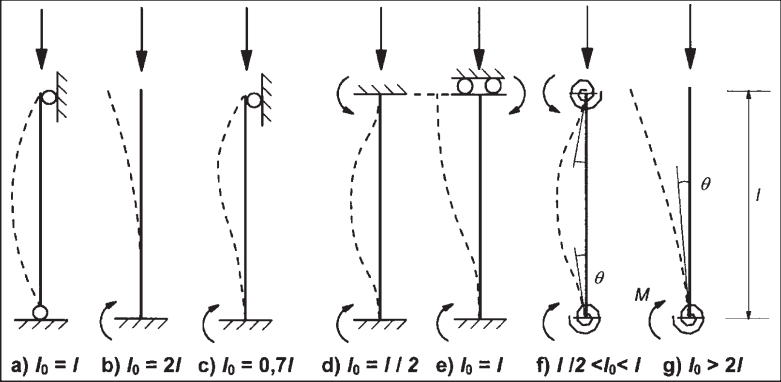
В СП 63.13330 коэффициенты расчетной длины внецентренно сжатых элементов (для колонн и для стен) приведены в пункте 8.1.17. В австралийском стандарте AS 3600-2001 эти коэффициенты описаны в пункте 10.5.4 главы 10.
Хочется отметить, что большая часть коэффициентов, даже для простых типов закрепления, в указанных документах отличается. Даже для самого простого типа закрепления, консольного стержня, принятый в наших нормах коэффициент 2 меньше чем в австралийском стандарте, там он равен 2.2.
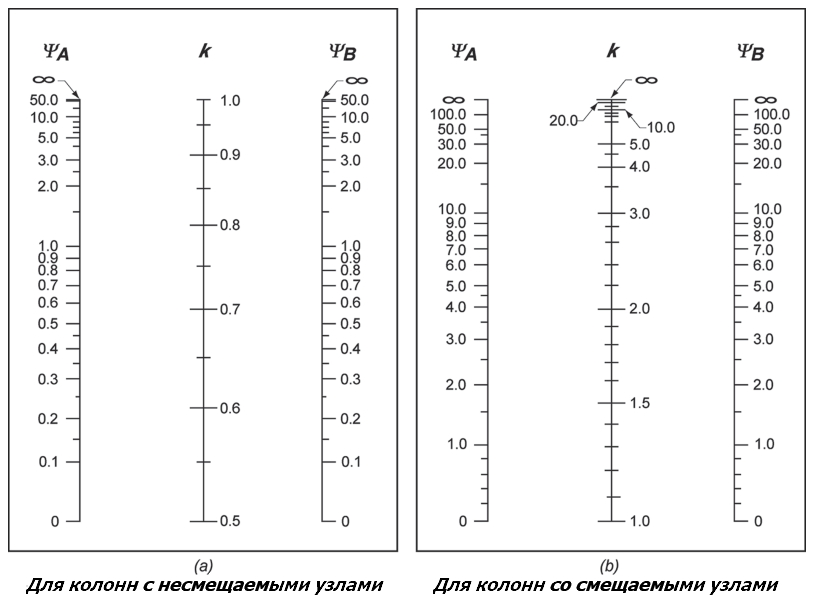
Коэффициенты расчетной длины для сложных типов закрепления, которые в СП 63 имеют точное значение (например, для элементов с несмещаемыми (с ограниченным поворотом) заделками на двух концах — 0.8, а для элементов с ограниченно смещаемыми податливыми (с ограниченным поворотом) заделками на двух концах — 1.2), в AS 3600-2001 определяют с помощью таблиц на рисунках 10.5.3(B) и 10.5.3(C) и зависят от коэффициентов закрепления y1 и y2, которые, для обычных прямоугольных каркасных зданий и сооружений, определяют по формуле:
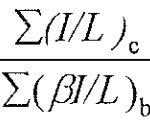
В числителе — суммарная жесткость в плоскости изгиба колонн, примыкающих к рассматриваемому узлу и жестко соединенных между собой;
В знаменателе — суммарная жесткость в плоскости изгиба плит или балок (или плит с балками), примыкающих к рассматриваемому узлу и жестко соединенных с колоннами.
Коэффициент бетта — коэффициент условия закрепления, приведенный в таблице 10.5.4, для условий закрепления балки или плиты (или плиты с балкой), на противоположном конце от рассматриваемого узла соединения колонны с плитой или балкой.

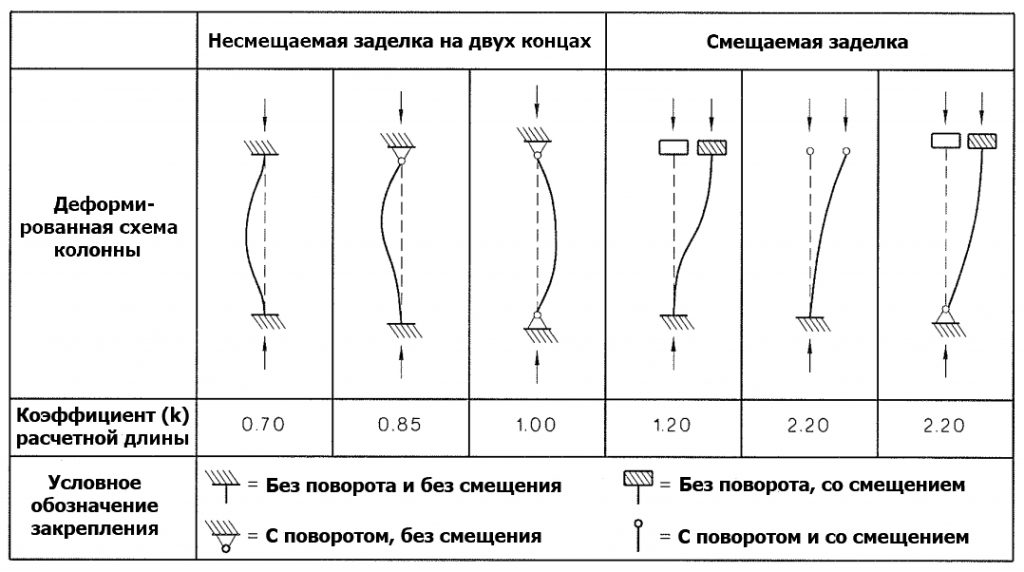
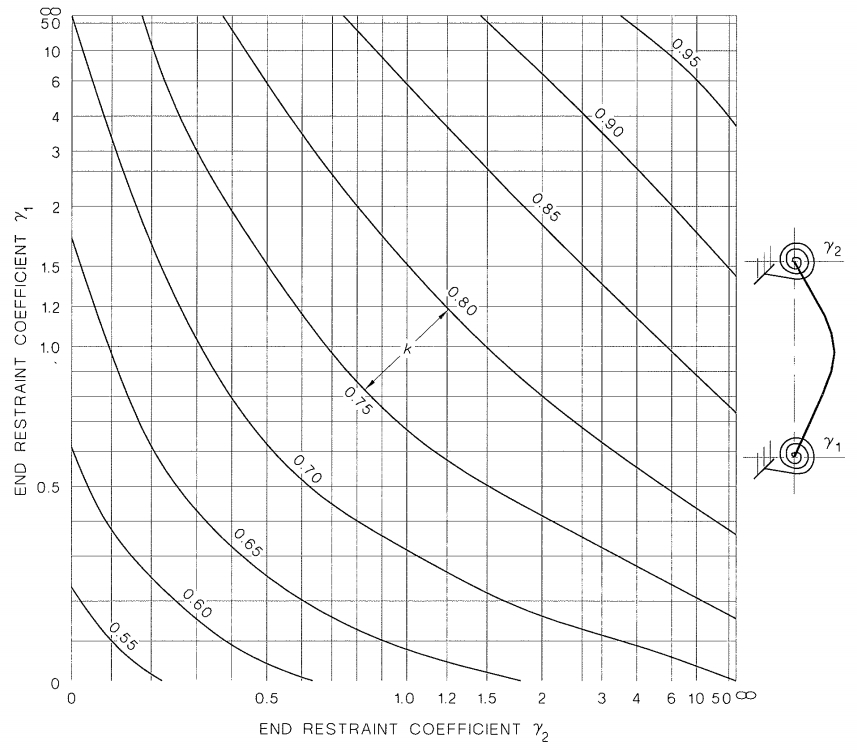
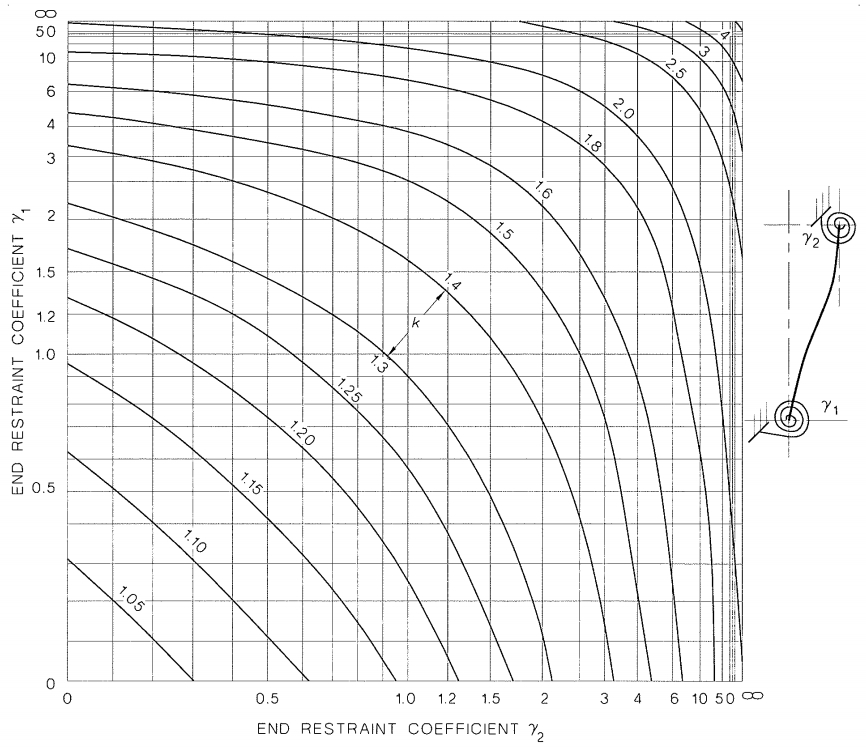
Как видно из рисунков 10.5.3 (B) и (C) австралийских норм коэффициенты расчетной длины не ограничиваются значениями 0.8 и 1.2 соответственно, которые указаны в СП 63, а могут существенно превосходить их, особенно в случае со смещаемыми податливыми закреплениями.
Расчетные длины для железобетонных стен в зависимости от типов закрепления приводятся в ТКП EN 1992-1-1-2009, в главе 12.6.5.1 «Гибкость колонн и стен».

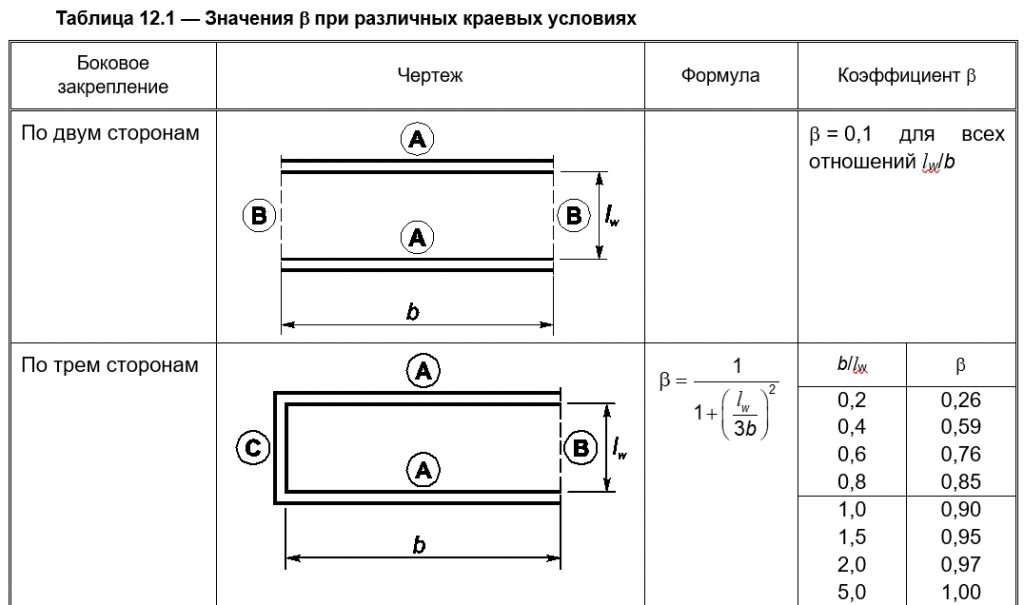
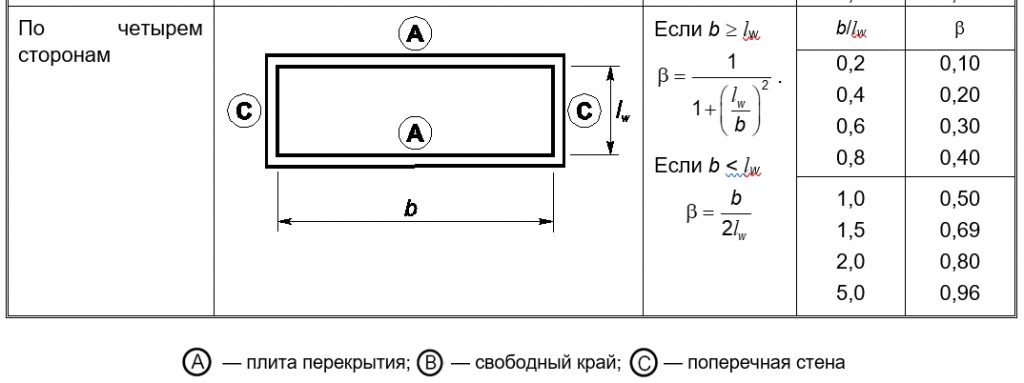

Определение расчетной длины стен также описано в «Руководство по проектированию конструкций и технологии возведения монолитных бескаркасных зданий. 1982 г.» в пункте 5.4.
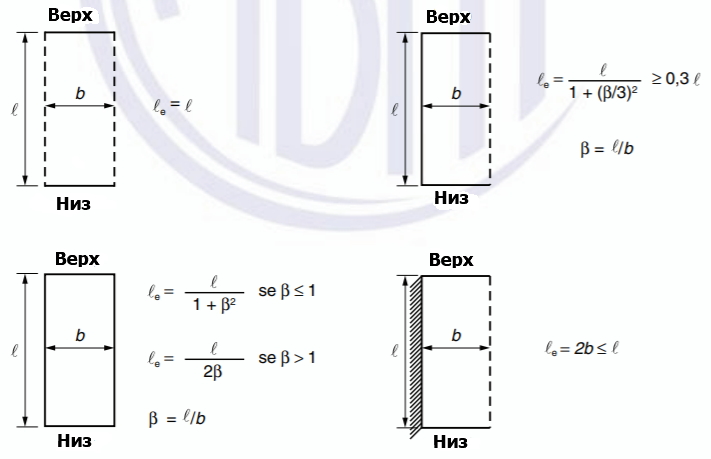

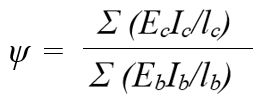
Коэффициент относительной жесткости на каждом из двух концов колонны
EсIc — суммарная жесткость колонн примыкающих к рассматриваемому узлу колонны;
EbIb— суммарная жесткость балок примыкающих к рассматриваемому узлу колонны;
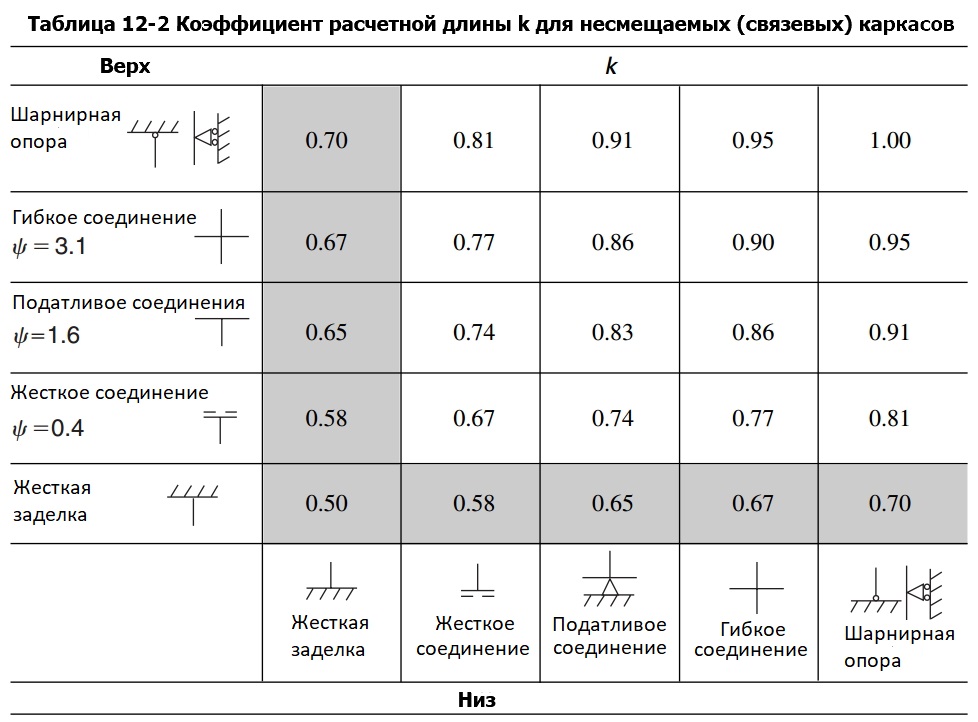
Коэффициенты из таблицы 12-2 используют в первом приближении, так как они не учитывают реальную жесткость узлов соединения колонн и плит, зависящую от фактического армирования и наличия трещин. В реальности, абсолютно жестких и абсолютно шарнирных узлов не бывает, поэтому в практике проектирования коэффициент пси принимают не менее 0.2 и не более 20. Коэффициент расчетной длины k в несмещаемых каркасах принимают не менее 0.6, а в смещаемых каркасах с закрепленными узлами колонн не менее 1.2.
Ссылки по теме статьи:
Материалы статьи взяты из диссертации Болгова А. Н. «Работа узлов сопряжения колонн из высокопрочного бетона с перекрытием в монолитных зданиях с рамно-связевой системой».
Количество высотных железобетонных зданий и небоскребов, во всем мире, увеличивается с каждым годом. Такие дома меняют внешний облик городов и приносят большую прибыль застройщикам. Они являются местом скопления большого количества людей и, в случае аварии, влекут за собой трагические последствия. С каждым годом высота подобных зданий становится все больше, но сведений, в нормативных документах, об особенностях их работы не так много. Этой статьей хочется обратить внимание к данной проблеме и привести те немногие материала, которые удалось найти по данному вопросу.
Высотные здания относятся к категории уникальных и к ним предъявляются повышенные требования безопасности. Колонны нижних этажей воспринимают большие нагрузки, поэтому их, часто, конструируют из высокопрочного бетона (тяжелого бетона класса В60…100), но плиты перекрытий, из-за экономии, конструируют из обычного бетона класса В25-В40. Как известно, проектирование жилых и общественных железобетонных зданий и сооружений следует вести в соответствии с СП 63.13330.2012 и СП 311.1325800.2017, однако, в этих нормативных документах нет указаний на особенности работы конструкций с отличающимися классами бетона.
В диссертации [1] автор указывает на следующее: «Последние экспериментальные данные о работе плит перекрытия из высокопрочных бетонов на продавливание показывают, что модель, принятая в отечественных нормах проектирования завышает фактическую несущую способность и требует корректировки. Применение узлов плит с колоннами из разной прочности приводит к появлению больших сжимающих усилий в нижних этажах, не учитываемых при расчете на продавливание». Он также обращает внимание на то, что, ни в каких нормах (в том числе зарубежных) не учитывается влияние на несущую способность верхней колонны.
Общие выводы диссертации:
«1. Проведенные исследования работы узлов перекрытия с колоннами разной прочности показали, что основными влияющими факторами на несущую способность узлов являются: отношение прочности бетона колонн и плиты (Rcol/Rpl); отношение размеров сечения колонн и плиты (h/с) и изгибающий момент со стороны плиты перекрытия.
2. Выполненные экспериментальные исследования работы моделей узлов показали, что наличие хомутов в узле, а также применение высокопрочной арматуры в колоннах повышает несущую способность узлов. При этом, наличие хомутов повышает пластичность узла при разрушении.
3. По результатам проведенных испытаний плит на продавливание установлено, что сжатие со стороны верхней колонны оказывает положительное влияние на несущую способность и жесткость плиты. Данные выводы до проведения дальнейших исследований можно использовать только для отношений (Rcol/Rpl), исследованных в работе.
4. Анализ экспериментальных данных по продавливанию позволил уточнить расчетные формулы отечественных норм, для случая симметричного продавливания, для плит перекрытий из высокопрочного бетона, а также плит с различным процентом армирования.
5. Выполненный сравнительный анализ численной модели, основанный на МКЭ с применением физически нелинейных КЭ и критериями прочности, с имеющимися экспериментальными данными работы узлов из разного класса бетона, показал её хорошее соответствие опытным данным. Это позволило использовать данную модель в дальнейших исследованиях работы узлов в условиях, трудновоспроизводимых в натурных экспериментах.
6. Численное моделирование работы промежуточных, крайних и угловых узлов позволило проследить их работу на всех стадиях нагружения, включая разрушение, а также установить, что разрушение промежуточных и крайних узлов имеет пластичный характер, в то время как угловые узлы разрушаются хрупко.
7. Так же на основе численного моделирования работы узлов было выполнено исследование влияния концентрации хомутов колонны в зоне узла, а также влияние высокопрочной арматуры на несущую способность узлов при сжатии. Установлено, что применение высокопрочной арматуры приводит к значительному повышению несущей способности промежуточных и крайних узлов, при этом изменяется характер разрушения крайних узлов с пластичного при обычной арматуре в колоннах, до хрупкого — с высокопрочной арматурой. Применение высокопрочной арматуры в угловых колоннах незначительно повышает несущую способность угловых узлов при сжатии.
8. В результате проведенных исследований даны предложения по расчету узлов плит перекрытий с колоннами из разного класса бетона на сжатие, в зданиях с рамно-связевой системой».
В диссертации приводятся формулы для расчета несущей способности узлов соединения колонн с плитой перекрытия для средних, крайних и угловых колонн из высокопрочного и обычного бетона, а также приводятся конструктивные мероприятия по улучшению работы данных узлов.
Хочется надеяться, что в СП 63, со временем, появятся требования, отражающие все особенности работы конструктивных элементов высотных зданий из высокопрочного и обычного бетона.
В качестве рекомендаций, на что нужно обращать внимание при проектировании зданий высотой более 75 м ниже приведена цитата из статьи Николая Никонова «О высотных зданиях и нормах» из журнала «Высотные здания», выпуск 1/2006:
«…над чем нужно работать:
● обоснования для научного сопровождения проекта, «вариантного проектирования»;
● обязательное привлечение геофизиков к начальным изысканиям, позволяющим в целом оценить пригодность участка для строительства, обосновать характер и объем последующих
инженерно-геологических работ;
● обследование близлежащих зданий и инженерных коммуникаций, доказательства необходимости их реконструкции;
● выявление особых условий строительства (изменение свойств несущего грунтового массива, высокий уровень грунтовых вод, приближенность объекта к постоянным источникам шума и вибраций, микросейсморайонирование и т.п.);
● установление степени ответственности сооружения, основных его характеристик – высоты, формы, необходимых свойств строительных материалов, системы безопасной эксплуатации;
выбор фасадной системы и инженерного оборудования, обеспечивающего минимально возможное энергопотребление;
● система контроля за разработкой проекта (расчеты «в две руки», трехстадийное проектирование, работа научно-технического и архитектурного советов и т.д.);
● обязательность бизнес-плана;
● включение в состав проекта раздела «Паспорт объекта и требования к эксплуатации»;
● обоснование поэлементного мониторинга. Перечисленное – абсолютные общности для всех сложных, т.е. уникальных объектов».
Журнал «Высотные здания» можно скачать из архива по ссылке.
Ссылки по теме статьи:
Как известно, разрушение изгибаемых железобетонных элементов по наклонным сечениям происходит при одновременном действии поперечной силы Q и изгибающего момента М.
При опирании плит на монолитные стены, при проверке наклонных сечений, вырезают полосу плиты шириной 1 м.
При превышении …. в бетоне образуется наклонная трещина (вызываемые главными растягивающими напряжениями), проходящая через всю зону растянутого бетона.
Наклонная трещина в толстых плитах при недостаточной длине верхней продольной арматуры может уходить за стержень
Процесс образования наклонной трещины
Вследствие неупругих свойств бетона касательные напряжения распределяются равномерно по сечению, поэтому наклонная трещина раскрывается примерно одинаково по всей длине. При разрушении происходит взаимное смещение частей элемента по вертикали.
По мере увеличения нагрузки, в поперечной арматуре растут напряжения, достигая расчетного сопротивления, а затем, в процессе текучести, наступает также предельное состояние либо бетона над наклонной трещиной, либо продольной арматуры. В первом случае разрушение бетона вызовет разрушение элемента в целом (от действия момента поворачиваются части элемента относительно центра тяжести сжатой зоны бетона над трещиной. При этом трещина раскрывается, развивается по высоте, сокращается сжатая зона бетона. Напряжения в бетоне достигают предельных и происходит разрушение элемента), хотя напряжения в продольной арматуре и не достигли предельных значений. Во втором случае (сечение продольной арматуры достаточно и обеспечена её надёжная анкеровка, что препятствует повороту обеих частей элемента. Разрушение по наклонному сечению происходит после достижения предельных значений в поперечной арматуре из-за среза бетона над наклонной трещиной. Обе части элемента смещаются друг относительно друга. Такое разрушение вызывается действием поперечной силой) нагрузка может расти и далее, пока не разрушится бетон над трещиной или не нарушится анкеровка продольной арматуры, находящейся под предельным напряжением. Возможен и третий вариант разрушения — при значительном насыщении элемента поперечной арматурой она не может достичь своих предельных сопротивлений и элемент разрушается от раздавливания бетона в середине высоты элемента, между наклонными трещинами (в тавровых и двутавровых элементах при малой ширине стенки). Во всех случаях исчерпание прочности элемента определяется совместным действием изгибающего и крутящего моментов, поперечной и продольной сил.
Расчет по сжатой и растянутой зонам наклонной трещины выполняют независимо один от другого. При этом для оценки прочности по сжатой зоне используют уравнения равновесия поперечных сил, а по растянутой — уравнение равновесия моментов в наклонном сечении, считая, что разрушение по сжатой зоне происходит при преимущественных деформациях сдвига, а по растянутой — при преимущественных деформациях поворота двух блоков, разделенных наклонной трещиной, один относительно другого.
В общем случае должна рассматриваться система трех уравнений равновесия в наклонном сечении — равновесия поперечных сил, равновесия моментов, равновесия продольных сил. Однако, такой методики в нормах, пока, нет, поэтому рассматривают раздельный расчет на действие поперечной силы и на действие момента в наклонном сечении. Кроме того, пока не известно, как влияют на прочность наклонного сечения величины моментов, поперечных и продольных сил, при совместном их взаимодействии…
Напряжения в продольной арматуре к моменту разрушения сечения, как правило, не достигают своих предельных значений, т.е. расчетных сопротивлений. Так как в этих стержнях достигается предел текучести по всей площади стержня, то в арматуре действуют лишь осевые усилия, а поперечные, «нагельные», являются весьма незначительными. Так как наклонные трещины имеют криволинейное очертание, то при смещении берегов трещины возникают силы зацепления выступов, находящихся на берегах трещин, кроме того поверхность бетона в наклонной трещине шероховатая, этот факт также помогает бетонным поверхностям зацепляться друг о друга.
При этом сумма проекций внешних сил на ось, нормальную к оси балки, численно равна поперечной силе в поперечном сечении, совпадающем со сжатой зоной, а момент внешних сил относительно центра сжатой зоны численно равен изгибающему моменту в том же поперечном сечении. При расчете определяют независимо друг от друга предельные величины поперечной силы и изгибающего момента. Усилия в наклонных и вертикальных элементах арматуры входят в оба уравнения; условно расчет ведут раздельно для поперечной силы и изгибающего момента, но к расчетным сопротивлениям наклонной и поперечной арматуры вводят понижающие коэффициенты условий работы.
Наклонные трещины в стенке появляются в случае исчерпания предельной растяжимости бетона. Деформации растяжения вызываются целым рядом факторов: действием главных растягивающих напряжений от внешних сил и усилий преднапряжения, неравномерной и стесненной усадкой бетона, температурными воздействиями. Кроме того, механические свойства бетона крайне неоднородны. Поэтому трудно заранее предвидеть, где появится первая трещина в бетоне. В дальнейшем вследствие концентрации напряжений у концов трещин они развиваются опять–таки в направлении наименьшего сопротивления. Таким образом, процесс возникновения и развития трещины в бетоне является случайным процессом, и хотя можно предвидеть общий характер трещинообразования, точное местоположение и угол наклона трещины предугадать невозможно.
Поэтому в расчет вводят самое опасное положение трещины, т. е. такое, при котором сопротивление наклонного сечения оказывается наименьшим. Условием этого является минимальное значение отношения Qпр/Q. Приближенно его часто заменяют условием, чтобы наименьшее возможное значение имела предельная поперечная сила Qпр.
Расчет внецентренно сжатых элементов производят так же, как для изгибаемых элементов, без учета влияния нормальной силы. Это довольно грубое упрощение идет в запас прочности, так как сжимающее усилие увеличивает сопротивление сжатой зоны бетона срезу.
Изменение распределения трещин в зависимости от отношения высоты сечения к пролету балки (от преобладающих наклонных трещин до преобладающих нормальных трещин при большом пролете)
Расчет наклонных сечений в большей степени актуален для балок, однако, существуют методики расчета наклонных сечений и монолитных железобетонных плит перекрытий, опирающихся на колонны квадратного (и близкого к квадратному) сечения. Данная методика, в частности, подробно описана в диссертации Шеховцова И. В. «Прочность и деформативность железобетонных плит без поперечной арматуры при продавливании». Суть метода основывается на предположении, что несущая способность плиты на продавливание может быть определена, как несущая способность перекрестных балок приведенной ширины от действия поперечных сил. Рассматривается случай разрушения по сжатой зоне бетона в результате среза бетона над наклонной трещиной каждой из балок.
Бывают и смешанные расчеты на продавливание и наклонные сечения, в частности, в серии Б1.020.1-7 допускается производить расчет только примыкающих к колонне ригелей, а расчет на продавливание не производить.
Рис.1 Различные типы примыкания ригелей к колонне. Область продавливания обозначена контуром «с». Расчет на продавливание заменяется расчетом наклонных сечений примыкающих ригелей
Ссылки:
Прямоугольные колонны (пилоны) шириной 200 — 300 мм, в последнее время, становятся все более и более популярными. Их популярность объясняется тем, что в сочетании со стенами из блоков толщиной 200 мм, они позволяют архитекторам создавать приемлемые, для покупателей квартир, планировочные решения, с шагом колонн до 6 м. При назначении шага колонн, одним из определяющих критериев является расчета на продавливание по действующему СП 63.13330.2018. Однако, указанный в СП63 расчет не учитывает некоторые факторы, которые могут заметно снижать несущую способность плит на продавливание (без поперечной арматуры).
Рис. 1. Схемы расчетных контуров поперечного сечения при продавливании плоских плит из СП 430.1325800.2018
Рис. 2. Схема распределения касательных сил в плите возле крайних пилонов в зависимости от отношения длины к ширине пилона
Особенности расчета на продавливание плит перекрытий прямоугольными колоннами описаны в нормах таких стран, как США (ACI 318R-14), Бразилия (ABNT NBR 6118:2014) и Европа (EN 1992-1-1-2009), однако, в советских и российских нормах не указано никаких различий, при расчете на продавливание перекрытий средними колоннами, с соотношением сторон 1/2…1/4. В нормах лишь учитывается небольшое отличие фактического распределения напряжений в арматуре от принятой для расчета, с помощью коэффициента 0,8. В рекомендуемом (на сегодняшний день) СП 52-103-2007, в пункте 5.7, говорится о том, что колонны с соотношением сторон менее 1/4 следует относить к стенам, т.е. продавливание таких вытянутых в плане пилонов (или простенков) следует рассчитывать по двум методикам: торцевые участки рассчитывают по методике продавливания плит возле торцов стен (методика описана в «НАУЧНО-ТЕХНИЧЕСКИЙ ОТЧЕТ по теме: Разработка методики расчета и конструирования монолитных железобетонных безбалочных перекрытий, фундаментных плит и ростверков на продавливание»), а длинные стороны вытянутого пилона (простенка) рассчитывают по наклонным сечениям (по СП63). Но для пилонов с соотношением сторон 1/2…1/4 никаких специальных требований не предусмотрено, такие пилоны следует рассчитывать по той же методике, что и квадратные колонны.
На рисунках 1-5 показаны примеры возможного разрушения плит при продавливании в общем случае.
Рис. 3. Картина разрушения плиты толщиной 250 мм без поперечной арматуры при продавливании колонной сечением 130х130 мм
Рис. 4. Картина разрушения плиты толщиной 250 мм без поперечной арматуры при продавливании колонной сечением 520х520 мм
Рис. 5. Картина разрушения плиты толщиной 320 мм без поперечной арматуры при продавливании колонной сечением 340х340 мм
Рис. 6. Картина разрушения плиты толщиной 400 мм без поперечной арматуры при продавливании колонной сечением 440х440 мм
Рис. 7. Основные схемы разрушения плит с поперечной арматурой при продавливании средней колонной: а) стандартный случай по поперечной арматуре, установленной в зоне продавливания; b) разрушение за зоной установки поперечной арматуры; c) разрушение по бетону, при превышении допустимого расстояния от грани колонны до первого поперечного стержня; d) разрушение всей армированной зоны; e) разрушение по бетону меду арматурными стержнями, при превышении допустимого шага стержней; f) разрушение от разрыва продольной арматуры.
Картинки 1-5 взяты с адреса: «https://docviewer.yandex.ru/view/201669561/?*=Vw4n%2FnpBpnJmq0PMg0yraiZCgzp7InVybCI6Imh0dHBzOi8vaW5mb3NjaWVuY2UuZXBmbC5jaC9yZWNvcmQvMTgwMjIxL2ZpbGVzL0VQRkxfVEg1NDA5LnBkZiIsInRpdGxlIjoiRVBGTF9USDU0MDkucGRmIiwidWlkIjoiMjAxNjY5NTYxIiwieXUiOiIyOTM1OTQxMzcxNDUwMjEwNjQ1Iiwibm9pZnJhbWUiOnRydWUsInRzIjoxNTI4NzE3NDk5OTMyLCJzZXJwUGFyYW1zIjoibGFuZz1lbiZuYW1lPUVQRkxfVEg1NDA5LnBkZiZ0bT0xNTI4NzE2ODM4JnRsZD1ydSZ0ZXh0PUNTQ1QlMjBpcyUyMGRldmVsb3BlZCZ1cmw9aHR0cHMlM0ElMkYlMkZpbmZvc2NpZW5jZS5lcGZsLmNoJTJGcmVjb3JkJTJGMTgwMjIxJTJGZmlsZXMlMkZFUEZMX1RINTQwOS5wZGYmbHI9MjEzJm1pbWU9cGRmJmwxMG49cnUmc2lnbj1jZGM4Y2JlMzAwMzUwNzZiMGJjZDNjZmIxNDUwZTY1YyZrZXlubz0wIn0%3D&page=1&lang=en»
Рис. 8. Разные виды поперечной арматуры (Источник: «http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1679-78252016001502970»)
а) неравномерное распределение нагрузки по плите перекрытия;
в) неравные пролеты плиты (так как такие плиты, чаще всего, имеют различное продольное армирование в ортогональных направлениях, которое влияет на распределение моментов и касательных напряжений).
В другой статье бразильских исследователей
В статье «Анализ напряженно-деформированного состояния плитных конструкций в приопорных зонах. О.В. Кабанцев, К.О. Песин, А.В. Карлин. 2017», авторы, проведя численные эксперименты, приходят к следующему выводу: «…численными исследованиями установлено, что разрушение по механизму продавливания может реализоваться на краевых зонах протяженных в плане опор плит перекрытий». В статье также написано, что один из авторов был свидетелем разрушения приопорной зоны плиты перекрытия у торца протяженной в плане опоры (стены) со схемой разрушения, соответствующей механизму продавливания.
В статье «СИЛОВОЕ СОПРОТИВЛЕНИЕ ЖЕЛЕЗОБЕТОННЫХ МОНОЛИТНЫХ ПЛОСКИХ ПЛИТ ПЕРЕКРЫТИЙ ПРИ ПРОДАВЛИВАНИИ КОЛОННАМИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ. В.Б. Филатов. 2012», автор указывает на то, что модель, принятая в СП 52 (и СП 63), с равномерным распределением напряжений по периметру расчетного контура удовлетворительно соответствует опытным данным, для круглых колонн и колонн с соотношением сторон не более 2. Автор пишет следующее: «При продавливании железобетонных плит колоннами прямоугольного сечения отмечено, что область наибольших деформаций в плите расположена у коротких граней колонны, вдоль длинных граней деформации плиты уменьшаются в направлении от углов колонны к ее центру. Причем эта особенность деформирования плиты по периметру колонны отмечается на всех стадиях испытания образцов, вплоть до разрушения» и предлагает считать длину условного расчетного контура, принимая в качестве граней короткую грань колонны, а также вводит коэффициент, который: «учитывает то обстоятельство, что напряжения среза, действующие в плите вдоль длинной грани колонны, либо запаздывают относительно тех же напряжений у коротких граней, либо вовсе не успевают достигнуть предельных значений, вследствие продавливания плиты на участках, прилегающих к коротким граням колонны«.
Уменьшение несущей способности на продавливание плит с прямоугольными колоннами (при соотношении сечения 1/5) также описано в » Shear Strength of Slab-Column Connections
under Gravity and Cyclic Lateral Loading. Sunendro Aris Sutanto Himawan. 2012″. В частности указывается, что при постоянном периметре продавливания, если отношение длинной стороны к короткой увеличивается, прочность на продавливание (сдвиг) уменьшается. Этот происходит из-за концентрации напряжений вдоль короткой стороны колонны».
В исследовании «“Punching Shear Strength of Slabs with Openings and Supported on Rectangular Columns. Teng, S.; Cheong, H. K.; Kuang, K. L.; and Geng J. Z., 2004”, проведенном совместно Наньянским технологическим университетом (NTU) и Строительно-монтажным управлением «Building and Construction Authority» (BCA) — Сингапур, было испытано 20 плит, с прямоугольными колоннами и отверстиями. В выводах приведены результаты, в которых указано, что усилия в плитах сконцентрированы главным образом вокруг более коротких сторон прямоугольных колонн.
В статье: «Punching of flat slabs supported on rectangular columns” ; Engineering Structures 77 (2014) 17–33» на основании четырех экспериментом показано отличие распределения сдвиговых напряжений в зависимости от сечения колонны и от её направления относительно нагруженного пролета.
Рис. 9. Распределение касательных напряжений и трещин в плите (Источник: «http://epubs.surrey.ac.uk/805957/1/ENGSTRUCT-Punching_rectangular%20columns_FINAL%20MANUSCRIPT.pdf.pdf»)
Рис. 10. Схемы определения критических зон плиты при разных типах сечений колонн (по DIN 1045-1)
Во всех перечисленных выше исследованиях и статьях общим является вывод о том, что при продавливании плит прямоугольными колоннами напряжения концентрируются вдоль коротких граней колонн (при направлении короткой стороны колонны перпендикулярно пролету плиты), что приводит к неравномерной схеме продавливания и, в результате, к снижению несущей способности плиты при данном расчете. Для квадратных колонн, при широкой стороне сечения, замечена концентрация сдвигающих напряжений на углах колонны.
Тем не менее, не смотря на большое количество экспериментальных данных, как было указано в начале данной статьи, на сегодняшний день нет полного и исчерпывающего понимания того, что и как (в какой мере) влияет на данный расчет, тем не менее, методики используемые в зарубежных нормах, в большинстве случаев, подтверждаются испытаниями и могут использоваться для проверки на продавливание плит прямоугольными колоннами.
Рис. 11. Примеры комбинированного армирования стыка плиты с колонной (Источник: «https://findpatent.ru/patent/230/2305159.html»). Использование комбинированного армирования позволяет лучше учитывать неравномерность распределения напряжений в плите в зоне ее опирании на прямоугольные пилоны с отношением сторон более 1/2. В частности, при резком повышение напряжений в плите возле узких торцов пилона (например, при неравномерном шаге колонн). Этот вариант армирования эффективен, если продавливание плиты вдоль узкого торца невозможно избежать установкой гибкой арматуры и нельзя увеличить толщину плиты или класс бетона. Примеры расчета ж/б сечений с жесткой арматурой приведены в «Руководство по проектированию железобетонных конструкций с жесткой арматурой»
В качестве примера далее приведены фрагменты текста зарубежных нормативных документов, в которых описаны особенности учета, при расчете на продавливание, прямоугольного сечения колонны.
«R8.4.4 Расчетное значение сдвигающих напряжений в плите вокруг колонны, должно соответствовать пункту 22.6.
8.4.4.1.1 Плиты должны быть рассчитаны на действие двусторонних сдвигающих напряжений возле колонн, в местах приложения сосредоточенных нагрузок и на участках действия реактивных сил в соответствии с 22.6.4.
22.6.1.2 Нормативная прочность на сдвиг для элементов, работающих на изгиб в двух направлениях, без поперечной арматуры, определяется:
vu = vc (22.6.1.2)
22.6.5.2 vc определяется в соответствии с Таблицей 22.6.5.2.
Для обычного тяжелого бетона коэффициент лямбда принимается равной единице.
f’c — расчетная прочность бетона при сжатии (по нормам США).
R22.6.5.2 Для квадратных колонн напряжение vc ограничивается значением пункта «а» Таблицы 22.6.5.2. Однако, тесты (комитета Joint ACI-ASCE Committee 426
1974) показали, что указанное значение является небезопасным, когда отношение β длинной и короткой сторон прямоугольной колонны, или загруженной области, больше 2. В таких случаях, значение 4, в пункте «а» (вокруг углов колонны или нагруженная область) заменяется на 2. Другие испытания (Vanderbilt 1972), указывают на то, что значение vc уменьшается по мере увеличения соотношения b0/d. Выражения в пунктах (b) и (с) Таблицы 22.6.5.2 были добавлены для учета этих двух эффектов».
6.4.3 Расчет на продавливание
(2) Следует выполнить следующие проверки:
а) Вдоль периметра колонны или периметра площади приложения нагрузки максимальное напряжение от продавливания не должно быть превышено:
vEd <= vRd,max
б) Поперечная арматура из условия продавливания не требуется, если
vEd = vRd,с
с) Если значение vEd превышают vRd,c для рассматриваемого контрольного сечения, необходимо предусмотреть поперечную арматуру от продавливания согласно 6.4.5.
(3) Если реакция опоры действует с эксцентриситетом по отношению к контрольному периметру, необходимо определить максимальное напряжение по формуле:
vEd = β (VEd / ui d),
где d — средняя полезная высота плиты, принимаемая равной (dy + dz)/2;
dy, dz — полезная высота плиты в направлениях y и z соответственно в контрольном сечении;
ui — длина рассматриваемого контрольного периметра;
β — определяется по формуле:
при одноосном изгибе β = 1 + k β (MEd / VEd) (ui / Wi),
здесь ui — длина основного контрольного периметра;
k — коэффициент, зависящий от отношения размеров колонны с1 и с2: его значение является функцией пропорции неуравновешенного момента, переданного поперечной силой и совместно изгибом и кручением (таблица 6.1);
Таблица 6.1 — Значения k прямоугольных площадей приложения нагрузки
|
с1/с2 |
<=0,5 | 1,0 | 2,0 | >=3,0 |
| k | 0,45 | 0,60 | 0,70 |
0,80 |
Wi — соответствует распределению поперечного усилия, представленному на рисунке 6.19, и является функцией основного контрольного периметра ui:
dl — приращение длины периметра;
е — расстояние от dl до оси, вокруг которой действует момент MEd
Рис. 12. — Распределение поперечного усилия при неуравновешенном моменте в узле «плита — внутренняя колонна»
В руководстве для проектировщиков к Еврокоду 2 про коэффициент β написано следующее: «При расчете силы сдвига принято считать, что такая сила распределяется равномерно по критическому периметру. В действительности это не так, в частности, в месте соединения плиты и колонны, где отмечается передача момента между плитой и колонной. Точный расчет может показать, что в таком случае распределение силы сдвига по периметру неравномерное, а сама сила сдвига сопровождается крутящими моментами. Результаты масштабных экспериментов показали, что продавливание значительно меньше там, где происходит передача моментов. Это свидетельствует о том, что продавливание — это не исключительно пластический феномен: сдвиг в предельном состоянии по несущей способности нельзя распределить по периметру полностью. Чтобы учесть эти факторы, в расчете при проектировании используется коэффициент, который является функцией геометрической формы критического периметра и прикладываемых моментов. EN 1992-1-1 предлагает использовать коэффициент β, который увеличивает среднее напряжение сдвига вокруг периметра».
Для прямоугольных колонн
где c1 — размер колонны параллельно эксцентриситету нагрузки;
c2 — размер колонны перпендикулярно эксцентриситету нагрузки.
Для внутренней прямоугольной колонны, при нагрузке, приложенной с эксцентриситетом по отношению к обеим осям, β определяется приближенно по формуле
где ey и ez — эксцентриситеты MEd/VEd, соответственно вдоль осей y и z;
by и bz — размеры контрольного периметра (см. рисунок 7).
Рис. 13. Контрольный периметры колонны прямоугольного сечения вокруг площадей приложения нагрузки
Примечание — еу определяется из момента относительно оси z, еz — из момента относительно оси у.
Рис. 14. Схема распределения трещин при расположении колонны в центре плиты (с равными пролетами)
Рис. 15. Снимок трещин на плите
Рис. 16. Углы наклона трещин по X
Рис. 17. Углы наклона трещин по Y
Рис. 18. Значения напряжений в аналитической модели
Рис. 19. Схема распределения трещин при расположении колонны возле края плиты (при неравных пролетах)
Рис. 20. Снимок трещин на плите
Рис. 21. Углы наклона трещин по X
Рис. 22. Углы наклона трещин по Y
Рис. 23. Значения напряжений в аналитической модели
Эксперимент описан в статье «ANALISE EXPERIMENTAL DE LAJES LISAS UNIDIRECIONAIS DE CONCRETO ARMADO AO PUNCIONAMENTO SIMETRICO OU ASSIMETRICO. Belem 2006».
Заключение.
Анализ вышеописанной литературы позволяет сделать следующие выводы:
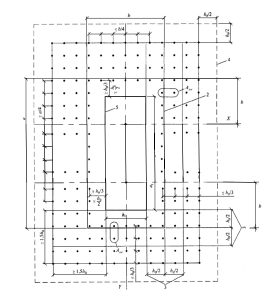 Рис. 24. Схема расположения поперечной арматуры пилона при соотношении его сторон 1/4-1/6 и величине продавливающей силы 1.3Fb,ult>Fпр>Fb,ult. При значениях продавливающей силы пилона 1.3Fb,ult<=Fпр<2Fb,ult поперечную арматуру следует устанавливать равномерно по всему контуру, включая среднюю часть пилона. В любом случае, следует отдельно проверять торцевые участки пилона, чтобы величина продавливающей силы Fпр на этих участках не превосходила 2Fb,ult. Продавливающую сила для проверки торцов принимается равной суммарной поперечной силе вдоль расчетного контура длиной 3b (см. картинку). Обозначения на картинке взяты из СП 63.13330.2012
Рис. 24. Схема расположения поперечной арматуры пилона при соотношении его сторон 1/4-1/6 и величине продавливающей силы 1.3Fb,ult>Fпр>Fb,ult. При значениях продавливающей силы пилона 1.3Fb,ult<=Fпр<2Fb,ult поперечную арматуру следует устанавливать равномерно по всему контуру, включая среднюю часть пилона. В любом случае, следует отдельно проверять торцевые участки пилона, чтобы величина продавливающей силы Fпр на этих участках не превосходила 2Fb,ult. Продавливающую сила для проверки торцов принимается равной суммарной поперечной силе вдоль расчетного контура длиной 3b (см. картинку). Обозначения на картинке взяты из СП 63.13330.2012 2. Ссылка на статью об осреднении поперечной арматуры;
4. Пример ручного расчета на сдвиг по ACI 318;
9. Расчет на продавливание с учетом формы разрушения. (Источник: «Журнал «Бетон и железобетон»»);
Разъяснение с ресурса:
http://www.normacs.info/answers/2240
«Спасибо за внимание к нашей работе. Новые карты районирования построены с повторяемостью расчетных значений веса снегового покрова один раз в 50 лет вместо 25-летней повторяемости, как было ранее.
При этом дополнительно к базе данных 50-80-х годов, по которой были построены старые карты, при определении расчетных значений веса снегового покрова были использованы также новые данные по всем имеющимся метеостанциям и постам за последние 30 лет.
Для значительной части территории страны снеговые нагрузки увеличились и при старых границах районов пришлось бы относить их к более высокому снеговому району, что не всегда было обоснованно.
Мы приняли новую градацию районов, равномерную, и сравнили полученные результаты. Они получились более приближенными к действительности при новой шкале снеговых районов и позволили в значительной мере сохранить прежние районы для наиболее населенной части страны.
Для некоторых районов при переходе к новой шкале снеговой район понизился, в том числе, для части Новосибирской области и г.Новосибирска.
Метеоданных для самого Новосибирска у нас нет, но есть данные по окрестным населенным пунктам во всех направлениях. Они не превышают оценки 210 кгс/м2.
Применять новые карты к СП 20.13330.2016 с районированием СП 20.13330.2011 не допускается.
Лебедева И.В., ЦНИИСК им. В.А. Кучеренко, лаборатория ЛНС»
Величина крутящего момента Tth сплошного сечения, до которой он не оказывает существенного влияния на прочность элемента при сдвиге и изгибе (вклад не более 3%) определяется по формулам таблицы 22.7.4.1(а), с учетом коэффициента понижения прочности ф (который определяется по таблице 21.2.1).
Формула расчета порогового значения крутящего момента Tth для сплошного сечения ж/б элемента без предварительного напряжения и продольной силы
f’c — расчетная прочность бетона при сжатии (по нормам США),
Величина f’с, используемая для расчета Tth и Tcr, не должна превышать 100 фунтов на квадратный дюйм (689.47589 кН/м2, 0.68948 МПа ). Из-за отсутствия данных испытаний и практического опыта работы с бетонами, имеющими прочность на сжатие более 10000 фунтов на квадратный дюйм, Кодекс устанавливает максимальное значение 100 фунтов на квадратный дюйм для использования при расчете прочности на кручение.
Аср — площадь ж/б сечения,
Рср — наружный периметр ж/б сечения,
— коэффициент снижения прочности, принимаемый равным единице для обычного (тяжелого) бетона и менее единицы для легкого бетона.
Nu — принимается со знаком «+» при сжатии и «-» при растяжении. (В российских нормах нет формул для расчета на кручение с учетом продольных сил, поэтому кручение в колоннах и балках рассчитывают без учета продольных сил, однако указаний на то, что продольные силы можно не учитывать также нет. В зданиях и сооружениях рекомендуется не допускать первую крутильную форму колебаний, так как эта форма приводит к появлению крутящих моментов в крайних (торцевых) колоннах здания).
Момент трещинообразования Tcr от действия крутящего момента определяется формулам таблицы 22.7.5.1
Формула расчета момента трещинообразования при кручении Tcr для сплошного сечения ж/б элемента без предварительного напряжения и продольной силы
Предел прочности при кручении Tn для железобетонных элементов без предварительного напряжения, а также преднапряженных, определяется по меньшему значению, полученному из двух формул
A0 — замкнутая область потока сдвиговых усилий, равная A0 = 0.85 A0h, где A0h — площадь сечения, огороженная осевыми линиями замкнутого хомута, установленного для восприятия крутящего момента,
A0h — общая площадь продольной арматуры, воспринимающей крутящий момент,
At — площадь сечения замкнутого хомута, установленного для сопротивления кручению (с шагом s),
fyt — номинальный предел текучести поперечной арматуры,
fy — предел текучести продольной арматуры (при отсутствии предварительного напряжения),
ph — периметр замкнутого хомута, сопротивляющегося кручению,
cot 0 — принимается не менее 30 град и не более 60 град.
При подборе площади хомутов в расчете учитывается площадь сечения «среза» хомутов, расположенных в непосредственной близости от грани поперечного сечения.
Арматура, рассчитанная на действие крутящего момента должна устанавливаться дополнительно к арматуре, рассчитанной из условия действия M, N, и Q на разных участках элемента.
Испытание ж/б колонны на действие крутящего момента
Если величина крутящего момента в рассматриваемом элементе выше Tcr, его можно уменьшить, при условии, что конструкция способна перераспределить усилия от кручения на другие элементы и не устанавливать дополнительную арматуру. При растрескивании, крутящий момент может уменьшиться в 3-6 раз и даже более. Этот факт, при возможности перераспределения, позволяет значительно уменьшать значение крутящего момента. Величина возможного перераспределения зависит от соотношения жесткостей: крутильной жесткости балки и изгибной жесткости примыкающих к ней элементов (например плиты). Чем меньше крутильная жесткость балки, тем больше будет угол её поворота и больше момент в примыкающей к ней плите.
Конструкции, в которых крутящий момент не может перераспределяться на другие элементы
Конструкции, в которых крутящий момент может перераспределяться на другие элементы
Элемент сопротивляется кручению аналогично пространственной ферме. После появления трещин прочность элемента обеспечивается за счет замкнутых хомутов, продольной арматуры и сжатых наклонных полос бетона.
Площадь бетона A0 после образования трещин принимается по внутренней части сечения, в пределах хомутов, равной 0.85 A0h.
В элементе без трещин, подвергнутом кручению, крутящий момент вызывает касательные напряжения (напряжения сдвига) в его поперечных сечениях. Они увеличиваются от нуля на оси элемента до максимальных значений на наружных гранях сечения. В прямоугольном сечении, касательные напряжения меняются от нуля в центре до максимума в центре длинных сторон. По периметру квадратного сечения напряжения сдвига изменяются от нуля в углах до максимума в центре каждой стороны.
Распределение касательных напряжений в прямоугольном сечении от действия крутящего момента
(картинка с ресурса: http://www.soprotmat.ru/kruch.htm)
Продольное усилие Ni, вызванное действием крутящего момента (сила N в стержне возникает при стесненном кручении, когда один из торцов стержня закреплен, а другой может свободно поворачиваться), распределяется в середины боковых сторон сечения. Каждый из угловых стержней воспринимает часть этой силы равную Ni/4. Суммарная продольная сила N действует вдоль оси элемента, поэтому продольная арматура должна быть равномерно распределена по сечению, так чтобы суммарный центр тяжести арматуры совпадал с центром тяжести элемента, и в каждом углу сечения должен располагаться продольный стержень, чтобы удерживать замкнутый хомут.
Преобразование поперечного усилия Vi в раскосное усилие обжатия Di и продольное усилие Ni
Если бетонный элемент воспринимает только крутящий момент, первые наклонные трещин образуются, когда максимальное растягивающее напряжение достигает предела прочности бетона. Элемент без арматуры при этом сразу разрушается. Продольные стержни балки без хомутов мало влияют на её прочность (при чистом кручении), поскольку они эффективны только для сопротивления продольной составляющей крутящей силы. Прямоугольная балка с продольными стержнями в углах и закрытыми (замкнутыми) хомутами может сопротивляться нагрузке и после растрескивания. При образовании трещин угол поворота увеличивается без увеличения крутящего момента, так как часть сил, ранее находившихся в бетоне, перераспределяется на арматуру, в этот момент, в статически неопределимых конструкциях происходит перераспределение усилий, поэтому крутящий момент может быть уменьшен. После растрескивания армированной балки, разрушение может произойти по нескольким причинам. Из-за разрыва хомутов, из-за разрыва продольной арматуры, (или того и другого одновременно), или из-за раздробления наклонных сжатых полос бетона с выпиранием арматуры.
При совместном действии изгибающего и крутящего моментов, к растягивающей силе от момента (на растянутой грани) нужно прибавить половину растягивающего усилия от кручения Ni/2. В сжатой зоне, сжимающие силы от изгибающего момента компенсируются частично (на участках со средней величиной момента) или полностью (на участках с максимальной величиной момента) растягивающими силами Ni/2 от крутящего момента.
При совместном действии крутящего момента и поперечной силы размеры сечения подбираются по формуле:
Vu — поперечная (сдвигающая) сила в поперечном сечении элемента,
Vс — прочность бетона на сдвиг,
ф — коэффициент понижения прочности при сдвиге равен 0,75,
bw — ширина прямоугольного сечения,
d — рабочая от сжатой грани сечения до центра тяжести растянутой арматуры,
Tu — величина крутящего момента в сечению,
ph — периметр замкнутого хомута, сопротивляющегося кручению,
A0h — площадь сечения, огороженная осевыми линиями замкнутого хомута, установленного для восприятия крутящего момента,
f’c — расчетная прочность бетона при сжатии,
Эта формула используется для контроля ширины раскрытия трещин от совместного действия крутящего момента и поперечной силы в сплошных ж/б сечениях. Проверка на раздробление сжатой наклонной полосы бетона не производится, так как раздробление происходит при более высоких сдвиговых напряжениях.
В общем случае, сначала, производиться проверка на действие изгибающего момента и назначается продольная арматура от изгиба. После этого производится расчет на действие поперечных сил и крутящего момента, и определяется дополнительная продольная и поперечная арматура от кручения и среза.
Ссылки:
Письмо с ресурса: http://scadsoft.com/problems
Письмо с ресурса: http://scadsoft.com/problems
Вопросы по некоторым схемам ветровых нагрузок
Письмо с ресурса: http://scadsoft.com/problems
Письмо с ресурса: http://scadsoft.com/problems
Письмо с ресурса: http://scadsoft.com/problems
Разъяснения НИИЖБ о возможности расчета массивных конструкций по СП 52-101-2003
Письмо с ресурса: http://scadsoft.com/problems
Рамные узлы соединения плит перекрытий со стенами — это неотъемлемая часть монолитных ж/б зданий. Для восприятия опорного момента в узле, верхнюю арматуру плиты необходимо надежно анкеровать в стену. В настоящее время используется три основных типа анкеровки верхней арматуры: анкеровка отгибом основной арматуры в стену (вверх или вниз), анкеровка с установкой Г-образных дополнительных стержней (также вверх или вниз) и анкеровка с установкой П-образных арматурных стержней (вместо Г-образных).
В чем же отличие между этими тремя типами анкеровки?
Определяющим фактором при выборе типа анкеровки является диаметр основной арматуры плиты и усилия в узле, от этого зависит длина анкеровки, возможный радиус загиба арматуры и необходимость дополнительной арматуры. В реальных конструкциях, из-за небольшой толщины стен (180-200 мм), требуемый нормами прямой участок сделать не удается, поэтому, в рамном узле арматура должна загибаться по увеличенному радиусу (10d(1-Lпрям.уч./Lанк), см. Пособие к СП 52), а не по обычному радиуса загиба по ГОСТу на арматуру (гарантирующему только целостность поверхности арматурного стержня). Это делается для того, чтобы избежать большой концентрации напряжений в бетоне в точке перегиба. В литературе также встречается анкеровка с установкой поперечных стержней в местах перегиба (см. «Standard Method of Detailing Structural Concrete»). Считается, что отгибаемый растянутый стержень, при растрескивании бетона в зоне загиба (смятии), зацепится за поперечный стержень, но это конструктивное мероприятие, методики расчета данного стыка нет.
Самой простой и экономичной является анкеровка с помощью отгибания основной арматуры плиты. Почему данный вид анкеровки не является единственным? Это связано с особенностью возведения ж/б конструкций, армирование плит начинается после бетонирования вертикальных конструкций и шов бетонирования под плитой не позволяет завести арматуру плиты на необходимую длину в стену. Самое очевидное и простое решение — отогнуть арматуру вверх, но это нельзя делать в плитах покрытия, так как вышележащих стен уже нет и арматуру плиты необходимо соединить с арматурой нижележащей стены для равномерной передачи момента с плиты на стену. Кроме того есть сложности и с местами, где располагаются дверные проемы, в этих местах также отогнуть арматуру вверх не получится.
Есть и другие причины, по которым нельзя обойтись только отгибанием основной арматуры, например, концентрация моментов во внутренних углах стен (лестнично-лифтовые блоки), на этих участках, как правило, требуется дополнительная арматура. В этом случае приходится считать необходимую длину отгиба и после этого принимать решение о типе дополнительной арматуры. Удобнее использовать U-образные арматурные элементы, так как нет необходимости устанавливать заранее в стены, в уровне перекрытий, дополнительные стержни для плиты и не нужно потом их отгибать в плиту. U-образные элементы можно монтировать вместе с армированием плиты перекрытия. Однако, применение U-образных элементов ограничено используемым диаметром арматуры. Если по расчету требуется дополнительно установить арматуру диаметром 20 мм, а плита толщиной 200 мм и менее, то U-образные элементы делать нельзя, так как в результате загиба может повредиться поверхность арматуры и уменьшится несущая способность рамного узла. В таких случаях используют L-образные стержни или приваривают стальные фиксаторы из поперечной арматуры или пластин. Кроме того, U-образные элементы (нижняя часть которых выходит за грань стены в зону нижней арматуры плиты) нельзя использовать, если по расчету требуется нижняя арматура, так как бетон передает сжимающие напряжения на арматуру и U-образный элемент будет воспринимать дополнительное усилие в нижней зоне плиты, т.е. стержень будет подталкиваться снизу и дополнительно растягиваться сверху. В таком случае, узел должен быть запроектирован из двух Г-образных элементов (один вверх — из нижней зоны плиты с анкеровкой в стену следующего этажа, а другой вниз — из верхней зоны плиты с анкеровкой в стену нижнего этажа). Такие узлы применяют на нижних этажах, где из-за осадок может требоваться нижняя арматура. Действующие нормы также разрешают использовать U-образные стержни для рамных узлов при раскрывающих узел моментах, когда нижняя грань плиты растянута. В этом случае необходимо добавлять дополнительный наклонных стержень (см. рис. 10.2 «б» СП 63 и рисунок J.4 «b» ТКП EN 1992-1-1-2009). U-образные стержни, можно использовать, если оба участка стержня растянуты (например в верхней зоне балок), т.е. U-образный стержень устанавливается параллельно плоскости плиты и не заходит в нижнюю зону, при этом он должен охватывать вертикальные арматурные стержни в стене или колонне. Также U-образные стержни применяют для обрамления торца плиты в зоне отверстия либо на свободных торцах плиты, в этом случае стена отсутствует и такой стержень воспринимает крутящий момент. Эффективнее всего использовать U-образные элементы, когда требуется верхняя арматура небольшого диаметра (8-10 мм), можно уменьшить шаг и диаметр арматуры, чтобы использовать U-образные элементы и тем самым упростить и ускорить возведение плит перекрытий. В любом случае, при использовании U-образных арматурных элементов, в местах загиба необходимо устанавливать (или приваривать) перпендикулярные стержни.
В каждом конкретном случае нужно подробно проанализировать все места, где необходимо отгибать арматуру и принять унифицированное решение, которое лучше всего подойдет для всех рамных участков плиты и с точки зрения трудозатрат, и с точки зрения стоимости и удобства монтажа. При балочных перекрытиях чаще всего отгибают верхнюю арматуру балки в стену или колонну, при безбалочных чаще всего устанавливают дополнительные U-образные элементы, но при этом уменьшают шаг, чтобы арматура была диаметром не более 10 мм. На плите покрытия устанавливать U-образные элементы не рекомендуется, в таких случаях отгибают арматуру стены, а если нужна дополнительная арматура, также устанавливают ровные стержни в стену до бетонирования, а потом отгибают в плиту. Минус данного способа в том, что трудно проконтролировать требуемый радиус загиба стержней.
Рис. 1. Фрагмент из британских норм по железобетону
Рис. 2. Еще один вариант анкеровки верхней и нижней арматуры
(Источник: https://www.buildinghow.com/el-gr/Προϊόντα/Βιβλία/Τόμος-Γ/Υλικά/Κάμψη-ράβδων-οπλισμού)
Рис. 3. Требования к Г-образным стержням в США
Фрагмент с ресурса: http://www.housingauthority.gov.hk/common/pdf/business-partnerships/resources/concrete.pdf)
Рис. 4. Анкеровка арматуры путем её отгиба при наличии прямого участка (l1) или при его отсутствии (из Пособия к СП 52-101-2003). В соответствии с пунктом 3.125 Руководства по конструированию 1978 г. дополнительные хомуты, препятствующие разгибанию стержня должны устанавливаться с шагом 100 мм
Рис. 5. Анкеровка арматуры на защемленных опорах (из Пособия к СНиП 2.06.08-87). а, е — путем запуска стержней на длину lan; б — с помощью привариваемых анкерующих стержней; в — путем приварки стержней к закладным деталям; г — путем отгибания стержней; д -путем отгибания стержней и постановки дополнительных хомутов; 1 — анкерующая деталь; 2 — закладная деталь; 3 — дополнительные хомуты, препятствующие разгибанию стержня; I — граница зоны анкеровки; II — бетонный массив; III — сжатая зона
Рис. 6. Два типа анкеровки с помощью загиба арматуры (из японского стандарта JSCE 2007): (а) — при загибе стержня по радиусу не менее 10 его диаметров, эффективной считается вся длина, включая изогнутую часть; (b) — если радиус загиба менее 10 диаметров стержня, но прямой участок за зоной загиба не менее 10 его диаметров, то прямой участок считается эффективным
Рис. 7. Пример определения радиуса загиба арматуры диаметром 25 мм по BS 8110 (Источник: «https://issuu.com/mebuild/docs/191283720-reinforced-concrete-desig»)
Рис. 8. Указание для радиуса отгибаемой арматуры из НиТУ 123-55 и СНиП II-В.1-62. Не смотря на то, что нормы разрешают отгибать арматуры в теле бетона по радиусу 10d, однако не рекомендуется размещать отгибаемую арматуру близко к наружной грани бетона: «Отгибать стержни, расположенные непосредственно у боковых граней балок, не рекомендуется. Стержни с отгибами располагают на расстоянии не менее 2d от боковых граней балки (Армирование элементов монолитных железобетонных зданий. Пособие по проектированию. Москва 2007)», это требование относится и к отгибаемой арматуре возле вертикальной или горизонтальной грани плиты перекрытия
Рис. 9. Допустимые диаметры оправки для арматурных стержней (из ТКП EN 1992-1-1-2009)
Рис. 10. Диаметры оправки арматуры разных классов из «Методическое пособие Проектирование железобетонных конструкций с применением сварных сеток и каркасов заводского изготовления. Москва 2016»
Рис. 11. Анкеровка с помощью анкерной пластины. Американские нормы (ACI).
Рис. 12. Горизонтальные и вертикальные хомуты воспринимают растягивающие усилия в узле и упрочняют узел в зоне анкеровки верхней арматуры (ACI).
Рис. 13. Дополнительные П-образные хомуты для анкеруемого в верхней зоне колонны арматурного стержня. Использование П-образных стержней для анкеровки продольной арматуры допускается пунктом 10.3.21 СП 63.13330.2018: «- с установкой дополнительных арматурных изделий в виде П-образных стержней с заведением концов в сжатую зону бетона на длину анкеровки»
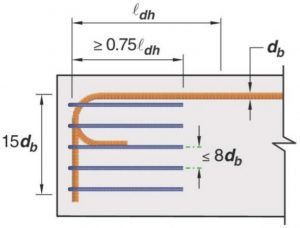 Рис. 14. Примеры установки дополнительной арматуры на длине анкеруемого стержня с отгибом, из ACI 318
Рис. 14. Примеры установки дополнительной арматуры на длине анкеруемого стержня с отгибом, из ACI 318
Рис. 15. Расположение хомутов перпендикулярно и параллельно арматурному стержню
Фрагмент книги с ресурса: https://www.slideshare.net/peakpilgrim/27-jun2015-splicing-of-reinforcement/p>
Рис. 16. Фрагмент из «Рекомендаций по проектированию железобетонных монолитных каркасов с плоскими перекрытиями. 1993 г.». Аналогичные узлы показаны и в «Сборник норм и правил по проектированию железобетонных безригельных каркасных зданий с плоскими плитами перекрытий. Краснодар — 2006»
Рис. 17. Фрагмент из книги «Руководство для проектировщиков к Еврокоду 2: проектирование железобетонных конструкций: руководство для проектировщиков к EN 1992-1-1 и EN 1992-1-2» о необходимости установки П-образных элементов на свободном краю плиты в зоне колонн
Рис. 18. Схема распределения напряжений в арматурном стержне.
Фрагмент книги с ресурса: https://www.slideshare.net/peakpilgrim/27-jun2015-splicing-of-reinforcement/p>
Рис. 19. Напряжения в арматурном стержне при при отгибе на 90 и 180 градусов.
Фрагмент книги с ресурса: https://www.slideshare.net/peakpilgrim/27-jun2015-splicing-of-reinforcement/p>
Рис. 20. Соединение балки с колонной.
Фрагмент книги с ресурса: https://www.slideshare.net/peakpilgrim/27-jun2015-splicing-of-reinforcement/p>
Рис. 21. Примеры образования трещин в результате экспериментов на выдергивание.
Фрагмент книги с ресурса: http://www.iitk.ac.in/nicee/wcee/article/1326.pdf /p>
Рис. 22. Распределение усилий в узле соединения балки с колонной.
(Источник: «http://www.ijirset.com/upload/2014/april/59_A%20Review.pdf»)
Рис. 23. Два типа трещин, которые могут образоваться в колонне при двух вариантах анкеровки арматуры балки
(Источник: «http://www.ijirset.com/upload/2014/april/59_A%20Review.pdf»)
Рис. 24. Распределение трещин в узле соединения балки с колонной при различных вариантах анкеровки арматуры балки.
Фрагмент книги с ресурса: https://www.concrete.org/publications/internationalconcreteabstractsportal.aspx?m=details&ID=51685465 /p>
Рис. 25. Распределение трещин в узле соединения балки с колонной при растянутом узле. Австралийские нормы.
Фрагмент книги с ресурса: https://books.google.ru/books?id=8tSYCgAAQBAJ&pg=PA664&lpg=PA664&dq=Australian+Standards+on+Concrete+Structures+(AS3600+-2001)&source=bl&ots=TKda9zBmin&sig=6c6M3Yx4xEFtgtqh_RANkG_Zwvk&hl=ru&sa=X&ved=0ahUKEwi_q6Puvv7TAhWIFZoKHXWGCJkQ6AEISzAG#v=onepage&q&f=false/p>
Рис. 26. Распределение трещин в узле соединения балки с колонной при сжатом узле. Австралийские нормы.
Фрагмент книги с ресурса: https://books.google.ru/books?id=8tSYCgAAQBAJ&pg=PA664&lpg=PA664&dq=Australian+Standards+on+Concrete+Structures+(AS3600+-2001)&source=bl&ots=TKda9zBmin&sig=6c6M3Yx4xEFtgtqh_RANkG_Zwvk&hl=ru&sa=X&ved=0ahUKEwi_q6Puvv7TAhWIFZoKHXWGCJkQ6AEISzAG#v=onepage&q&f=false/p>
Рис. 27. Распределение напряжений в расходящемся узле
Источник: «https://www.sciencedirect.com/science/article/pii/S1687404814000996»
Рис. 28. Пример армирования жестких узлов из СП 63.13330.
Рис. 29. Пример армирования жестких узлов из ТКП EN 1992-1-1-2009.
Испытание рамного узла соединения балки и колонной большого сечения
Рис. 30. Схемы армирования угловых сопряжений
железобетонных конструкций (из Пособия к СНиП 2.06.08-87); а — при наличии сжатой арматуры; б — при отсутствии сжатой
арматуры; в — при массивных конструкциях; 1 — сжатая арматура; 2 — сварка; 3 — армосетки; 4 — неравнобокие уголки (приварить)
Рис. 31. Примеры армирования наклонных ригелей.
Фрагмент взят с ресурса: http://detailsconstructifs.cype.fr/FIX130.html
Рис. 32. Схема армирования узла сопряжения наклонного ригеля а — при угле сопряжения менее 160 град, б — то же при угле сопряжения более 160 град (Руководство по конструированию 1978 г)

Рис. 33. Фрагмент из книги В. И. Мурашова «Расчет железобетонных элементов по стадии разрушения», 1938 г.
Рис. 34. Схема определения требуемой длины изогнутой части стержня в узле, зависящей от значения требуемой величины анкеровки ld и меньшим из углов между осью одного из растянутых стержней и равнодействующей усилий С3 (ACI 318-19)
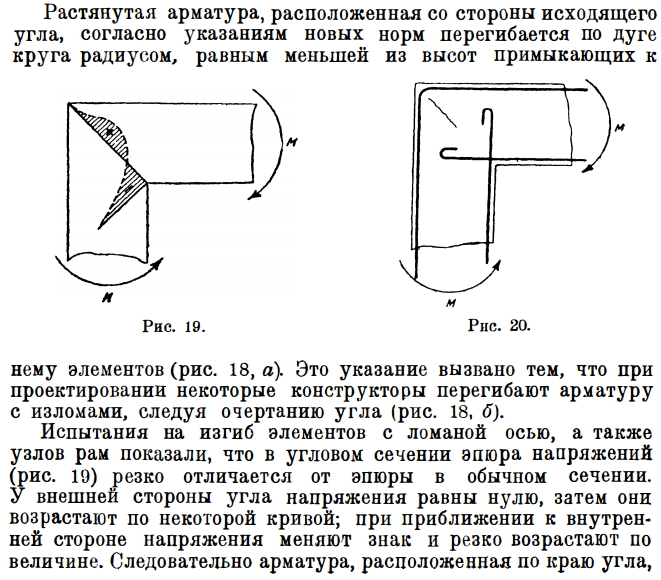

Рис. 35. Фрагмент из книги В. И. Мурашова «Расчет железобетонных элементов по стадии разрушения», 1938 г.
Рис. 36. Из книги: «ЖЕЛЕЗОБЕТОН его расчет и проектирование. Рудольф Залигер. Москва 1931 г.»
Рис. 37. Стык Г. П. Передерия: а — при осевом растяжении плиты; б — при изгибе. Руководство по проектированию подпорных стен и стен подвалов для промышленного и гражданского строительства
Аналог стыка Передерия используется при строительстве сооружений гражданской обороны (убежищ) в Швеции. Применение этого стыка позволило строить ж/б убежища внутри существующих зданий, применять сборные конструкции и сократить время строительства данных сооружений. Также он используется при строительстве тоннелей. (Данный стык может также применяться, например, при строительстве подземных паркингов из сборных элементов). Выполнение арматурных П-образных деталей на заводе позволяет уменьшить ошибки, связанные с гнутьем арматуры больших диаметров, так как увеличение диаметра приводит к увеличению радиуса загиба, что, в условиях обычных строительных площадок, часто приводит к нарушениям величины радиуса загиба арматуры.
В статье: «Structural Behaviour in Concrete Frame Corners of Civil Defence Shelters. Non-linear Finite Element Analyses and Experiments. Morgan Johansson. Sweden 2000» автор описывает проведенное в Швеции экспериментально-аналитическое исследование стыка железобетонных плит со стенами, в котором показывает, отличия в работе стыка при разном типе армирования. Далее приводятся фрагменты данного исследования.
Рис. 38. Стыки (а) и (b) были рекомендованы к использованию в шведских нормах проектирования убежищ, стык (c) — новый тип стыка, который предлагает автор исследования, вместо двух прежних стыков
В статье автор обращает внимание на требование шведских норм о величине максимального армирования узла для возможности пластической работы стыка и перераспределения усилий, чтобы большие усилия не концентрировалось в одном месте конструкции и не происходило хрупкого разрушения. Это особенно важно для сооружений гражданской обороны, на которые действуют импульсные (мгновенные) нагрузки большой силы. Поэтому одной из задач исследования была задача уменьшения количества арматуры в данном узле с сохранением несущей способности.
Рис. 39. Примеры конструкций с рамными узлами
Расходящийся угол
При рассмотрении расходящегося угла очевидным является наличие трещины с внутренней стороны угла, в точке соединения конструкций, однако, при работе узла возникает и вторая, диагональная, трещина. Усилия сжатия, как бы упираются во внешний угол и растягивающие усилия отсоединяют внутреннюю часть узла от наружной, и, при отсутствии там арматуры, появляется диагональная трещина.
Рис. 40. Пример образования диагональной трещины при неправильном армировании расходящегося угла
Рис. 41. На рисунке (а) показана ферменная идеализация распределения напряжений в расходящемся узле, описанная Нильссоном в 1973 г., на рисунке (b) показано распределение напряжений, сделанное автором исследования с заменой параболической (экспериментальной) эпюры напряжений на треугольную
Одним из вариантов решения проблемы образования диагональной трещины отрыва является установка диагональной арматуры, соединяющей наружный и внутренний углы. Однако, такое решение не в полной мере решает проблему, диагональная арматура находится на некотором расстоянии от грани бетона и, при больших усилиях, трещина образуется с наружной стороны арматуры. Кроме того, установка диагональных хомутов затруднительна при соединении плиты со стеной, поэтому это решение чаще применяется при соединении балок с колоннами, при относительно небольших усилиях.
Рис. 42. На рисунке (а) показана дополнительная диагональная арматура, на рисунке (b) показана трещина с наружной стороны угла
Решить проблему образования диагональной трещины можно также с помощью замены Г-образных стержней на U-образные. При этом происходит обжатие бетона внутри петель и диагональная трещина смещается (выдавливается) в сторону наружного угла, в результате происходит откол бетона за арматурой, по аналогии с узлом с установленными диагональными хомутами.
Диагональные стержни сдерживают развитие первой трещины с внутренней стороны угла и таким образом препятствуют распространению трещины за пределы сжатой арматуры, т.е. способствует повышению общей несущей способности узла. По экспериментальным исследованиям получено то, что площадь наклонных стержней должна равняться половине площади U-образных стержней.
Рис. 43. На рисунке (а) показано армирование в виде петель, на рисунке (b) показано армирование в виде петель с диагональным стержнем
Рис. 44. На рисунке (а) показана схема с порядком образования трещин с 1-ой по 4-ю, при испытаниях узлов с петлевой арматурой, на рисунке (b) показано распределение трещин в испытанной конструкции
Сходящийся угол
В узлах со сходящимися моментами разрушение может происходить по следующим причинам:
а) смятие бетона с внутренней стороны угла в зоне сжатого бетона (происходит при усиленном армировании и невысоком классе бетона);
б) раздавливание диагональной сжатой полосы в пределах угла (может произойти при коэффициенте армирования узла более 0,24);
в) скол бокового бетонного покрытия в соединениях ригелей с колоннами, что приводит к выходу из работы арматуры (может произойти при большом диаметре отгибаемой арматуры и маленьком защитном слое бетона до боковых поверхностей. Проблема более актуальна для соединения ригеля с колонной, чем для соединения плиты со стеной).
Скол бокового защитного слоя бетона происходит при отгибе арматурного стержня, в месте отгиба, там возникают радиальные сжимающие напряжения, которые приводят к появлению растягивающих напряжений, которые пытаются отколоть бетон в плоскости изгиба. Величина раскалывающих напряжений зависит от предела текучести стали, диаметра арматурного стержня и его радиуса загиба. В петлевых стыках напряжения скола выше чем в Г-образных стержнях. Чтобы уменьшить напряжения скола перпендикулярно изгибу можно использовать диагональные хомуты от наружного угла к внутреннему, продольные стержни внутри петель или увеличенный защитный слой.
Рис. 45. Пример скола бокового защитного слоя при испытаниях рамного стыка со сходящимися моментами
Рис. 46. На рисунке (а) показана схема распределения радиальных сжимающих напряжений в месте загиба арматурного стержня, на рисунке (b) показана возможная откалывающая защитный слой бетона трещина в плоскости изогнутого стержня
Рис. 47. Правильное и неправильное расположения стыков арматуры при использовании наклонных стержней
Вместо наклонных стержней можно использовать дополнительные петли, площадью не менее 35% от площади основных петель.
Рис. 48. На рисунке (а) показаны хомуты, приваренные к наружной анкерной пластине, на рисунке (b) показан фибробетон в месте заделки углового стыка
Для более полного использования петлевой арматуры в стыках со сходящимися моментами автор исследования рекомендует использовать петли из арматуры небольшого диаметра, а угол заделывать прочным фибробетоном с количеством фибры не менее 1%. Также, можно использовать пластины с наружной стороны угла с приваренными диагональными хомутами, для избежания откалывания защитного слоя бетона за зоной установки хомутов.
Аналогичное исследование расходящегося узла с различным армированием описано в статье: «REINFORCEMENT DETAILING FOR OPENING CORNERS. Prof. Roshan Lal, Dr. N.P.Devgan, Dr. Bhupinder Singh, Dr. S.P.Singh. Roshan Lal, 4 (6): June,2015». Авторы статьи приводят результаты экспериментального исследования рамного узла с 4-мя видами армирования и делают вывод о том, что максимально эффективным является тип армирования с петлей и диагональным стержнем.
Рис. 49. Четыре вида армирования, которые исследовались в эксперименте с расходящимся узлом. Тип 1 — без диагональной арматуры, с разрывом и анкеровкой нижней арматуры в верхнюю зону; Тип 2 — без разрыва верхней и нижней арматуры, но с диагональной шпилькой, соединяющей арматуру; Тип 3 — с пересекающимися П-образными арматурными элементами (стык Передерия); Тип 4 — с петлей нижней арматуры и диагональным стержнем, анкерующимся в зоне верхней арматуры
Рис. 50. Таблица с результатами испытаний 4-х типов узлов. Максимально эффективным оказалось армирование Тип 4, коэффициент эффективности узла 93,5%
Рис. 51. Узел Тип 4 соответствует узлу из СП 63.13330.2018 рекомендуемого для расходящихся узлов
Рис. 52. Три стадии работы узла Тип 4. Стадия 1 — бетон работает в упругой стадии, угол не растрескивается, напряжения воспринимаются бетоном и частично арматурой; Стадия 2 — в углу появляется трещина, усилия с бетона переходят в арматуру, затем образуется диагональная трещина, зона напряжения сдвигается к внешней стороне угла и диагональный стержень помогает углу сопротивляться отсоединению от внешней стороны; Стадия 3 — диагональная трещина резко поворачивается в сторону сжатия в диагональном направлении и узел разрушается
Авторы другой статьи «Behaviour of nodal regions of reinforced concrete frames subjected to opening moments and proposals for their reinforcement Stefano Campana, Miguel Fernández Ruiz, Aurelio Muttoni» (источик: «https://infoscience.epfl.ch/record/186974») также провели серию экспериментов с целью определения зависимости поведения расходящихся узлов от вида их армирования и угла наклона элементов узла. В конце статьи приводятся формулы для определения количества требуемой поперечной арматуры для узла, указанного в СП 63.13330.2018, с наклонной поперечной арматурой.
Рис. 53. Рамный узел с наклонной арматурой из СП 63.13330.2018 рекомендуемый для расходящегося узла
Рис. 54. Fw — усилие в поперечной арматуре
Рис. 55. pw — требуемая площадь поперечной арматуры
![]() Рис. 56. Определение коэффициента перераспределения усилий в узле
Рис. 56. Определение коэффициента перераспределения усилий в узле
Рис. 58. Различные виды армирования исследуемых узлов и схемы образования трещин в них. Сводная таблица результатов экспериментов (коэффициент эффективности узла принят, как отношение момента MR, при котором узел разрушился к аналитическому моменту Mflex, который может воспринять узел по расчету)
Ссылки:
1. Ccылка №1 по теме статьи;
2. Ccылка №2 по теме статьи;
3. Ccылка №3 по теме статьи;
5. Вебинар о различных видах узлов железобетонных конструкций и о распределении напряжений в них;
6. Пример расчета рамного узла с отверстием в программе IDEA StatiCa;
7. Статья об экспериментально-аналитическом исследовании работы жесткого стыка ригеля с колонной;
8. Проект СТО на петлевые стыки;
Поперечная арматура колонн с удлиненной стороной (пилонов) — это неотъемлемая часть их армирования. В таких колоннах возникают большие моменты вдоль длинной стороны и большие поперечные силы. Вертикальные стержни сгущают на краях и расставляют в средней части сечения с шагом не более 400 мм. Возникает вопрос, что выбрать в качестве поперечной арматуры? Многие конструкторы армируют пилоны четырехсрезными, шестисрезными и более «срезными» хомутами, принимая их одного диаметра и делая их одинакового размера. Кто-то, вместо нескольких хомутов ставит один хомут, а в средней части ставит шпильки. В чем отличие армирования хомутами от армирования шпильками?
В большей степени выбор типа армирования зависит от напряженного состояния пилона и от необходимой по расчету поперечной арматуры (величины поперечной силы). Общее требование — все сжатые стержни, расположенные у грани элемента, должны быть надежно скреплены арматурой от выпучивания (выкалывания защитного слоя бетона, при потере устойчивости сжатого стержня). Квадратные колонны с размером сторон до 400 мм включительно принято армировать хомутами, так как шпильками менее удобно (продольные стержни будут болтаться при монтаже). Кроме того, в колоннах часто возникает крутящий момент, а при действии крутящего момента хомут должен быть замкнутым.
Если по расчету требуется поперечная арматура диаметром d10 мм или d12 мм, то шпильки из таких диаметров делать не принято, но если по расчету достаточно одного охватывающего хомута, то, чтобы соблюсти конструктивные требования, можно поставить для средних стержней шпильки из арматуры d6 мм или d8 мм (с шагом не более 400 мм), и сэкономить на поперечной арматуре (не делать четырехсрезные или шестисрезные хомуты одного диаметра). В любом случае, все крайние стержни должны быть охвачены хомутом, а чем захватывать средние должен решить сам конструктор.
Единственное, на что стоит обратить внимание при выполнении требования п. 10.3.15 СП 63.13330, это на шаг шпилек, охватывающих вертикальную арматуру. Как известно, вертикальные стержни при сжатии могут терять устойчивость и выпучиваться в сторону меньшего расстояния до грани колонны, поэтому в нормативных документах (в частности, в пункте 10.3.14 СП 63.13330) указано максимальное расстояние между хомутами (или поперечными стержнями), которые удерживают вертикальный стержень от выпучивания по высоте колонны, это расстояние для внецентренно сжатых линейных элементов (т.е. колонн) равно 15 диаметров вертикального стержня. В СП 430 также указано про шаг поперечной арматуры в зоне нахлеста, для колонн, равном 10 диаметров вертикальной арматуры. Шаг поперечной арматуры равный 10d также предусматривается, если по расчету вдоль одной из граней колонны требуется установка более 1,5% сжатых стержней, тогда шаг поперечной арматуры не должен превышать 10d по всей высоте пилона (если площадь более 1,5% требуется по всей высоте пилона), об этом написано в СП 63. Но кроме максимального расстояния по вертикали в нормах прописано и про максимальное расстояние по горизонтали между загибами хомутов (или шпилек), относительно которых он может гарантированно удерживать вертикальный стержень от выпучивания при потере устойчивости. Как было указано выше, это расстояние прописано в пункте 10.3.15 СП 63.13330 и равно 400 мм. Кроме величины 400 мм, в СП 63 также указано, что вертикальные стержни должны быть охвачены поперечной арматурой через один стержень, т е. при шаге вертикальных стержней 100 мм на средней ширине пилона 400 мм должны быть охвачены 3 вертикальных стержня, крайние ряды и один средний ряд. Из большого опыта проектирования колонн, сложившегося еще в прошлом веке, можно сделать вывод, что колонны принято армировать замкнутыми хомутами через один вертикальный стержень. Тем не менее часто бывает ситуации, при которых по расчету не требуется поперечная арматура в колонне, например на средних этажах многоэтажного дома. В таких случаях поперечная арматура устанавливается только конструктивно, чтобы предотвратить выпучивание вертикальных стержней, поэтому замкнутые хомуты можно заменить шпильками. Тем не менее один общий замкнутый хомут, охватывающий все стержни должен быть установлен, а если вдоль грани колонны больше 4-х вертикальных стержней, то замкнутых хомутов должно быть не менее 2-х, но остальные вертикальные стержни можно охватывать шпильками. Шпильки в таком случает должны охватывать и вертикальный стержень и сам хомут (см. п. 10.4.3 СП63).
В нормативных документах по железобетону разных стран встречаются отличии в расстановке поперечных стержней. Например, в строительных нормах Индии поперечные стержни устанавливают, если расстояние между вертикальными стержнями более 75. Промежуточный вертикальный стержень можно не охватывать шпилькой, если он расположен на расстоянии меньшем или равном 75 от соседних и соседние стержни охвачены замкнутыми хомутами. В американских нормах требования менее строгие, там достаточно установить промежуточные шпильки с шагом не более 14 дюймов (35.56 см). В российских нормах, как было написано выше, требования еще менее строгие, допускается 400 мм между отгибами, при этом, если ширина грани менее 400 мм, то на внутренние два стержня шпильки можно не ставить.
В индийских нормах расстояние между загибами хомутов, при наличии неохваченного хомутом вертикального стержня равно 150 мм, в российских нормах 400 мм (но про неохваченные стержни ничего не сказано)
Расстояние xi по американским нормах равно 14 дюймам (35,56 см), при этом, судя по рисунку из норм, допускается один неохваченный вертикальный стержень
Расположение поперечных связей в широких колоннах (из норм по проектированию в Японии. 2007 г.)
Конструкция пространственных арматурных каркасов в сжатых элементах (картинка из «Методического пособия. Расчет железобетонных конструкций без предварительно напряженной арматуры к СП 63.13330.2012. Москва 2015)
Если сечение пилона сильно вытянуто в плане, то в соответствии с пунктом 10.4.6 СП 63.13330: «Армирование пилонов, занимающих по своим геометрическим характеристикам промежуточное положение между стенами и колоннами, производят как для колонн или как для стен в зависимости от соотношения длины и ширины поперечного сечения пилонов», т. е. пилоны с отношением сторон сечения менее 4 армируют как колонны, а с отношением более 5 армируют как стены. Также в соответствии с пунктом 5.7 СП 52-103-2007: «…Прямоугольные колонны (пилоны) с вытянутым поперечным сечением имеют соотношения b/a<4 или hэт/b>4. Более вытянутые в плане колонны следует относить к стенам» такие пилоны относят к стенам и для них действуют требования для стен, а именно, указанное в пункте 10.4.3 требование о соединении (охвате) поперечными связями (шпильками) одновременно и вертикальной, и горизонтальной арматуры, а также другие конструктивные требования, указанные в пункте 5.25 «Методическое пособие. Расчет железобетонных конструкций без предварительно напряженной арматуры. К СП 63.13330.2012» или Пособии к СП 52-101-2003. О принадлежности пилона к стенам или колоннам также указано в главе 5.3.1 (7) ТКП EN 1992-1-1-2009: «Колонной считается элемент, высота поперечного сечения которого не более его четырехкратной ширины, а общая длина составляет не менее его трехкратной высоты. В других случаях она рассматривается как стена».
В проектировании часто используют прямоугольные сечения колонн (пилоны), которые, по своим функциям в работе каркаса здания принципиально ни чем не отличаются (не считая увеличения жесткости в сторону вытянутого сечения) от квадратных колонн, однако, при моделировании возникает вопрос, как такие колонны (пилоны) лучше моделировать.
В разных рекомендациях к расчетным программам говориться о том, что моделировать такие колонны нужно в зависимости от соотношения сторон сечения; если меньшая сторона прямоугольной колонны меньше в 3 раза (или в 5 раз, в зависимости от рекомендаций в различных расчетных программах) большей стороны сечения, то моделировать нужно пластинчатыми элементами, в противном случае — стержневыми. В частности, в СП 52-103-2007, в пункте 5.7 говорится о соотношении сторон сечения и высоты колонны к большему размеру сечения — 1/4. При таких соотношениях, распределение напряжений в сечении перестает быть равномерным, как в стержневых элементах.
При выполнении общего, прикидочного, расчета каркаса для оценки общих параметров здания (предварительная расстановка диафрагм жесткости, проверка перемещения верха здания, осадки, крена и т.п.), принципиального отличия в моделировании нет. Если же предварительные расчеты выполнены и интересуют, например, усилия в плите перекрытия в зоне пилонов, то их лучше моделировать пластинами, а квадратные колонны — стержневыми элементами с «пауком» (стержнями повышенной жесткости в теле колонны) или абсолютно жестким телом (АЖТ); если же интересуют усилия в самой колонне (пилоне), то моделировать удобнее стержнями (но также с АЖТ).
При моделировании колонны стержневыми элементами, в результате расчета, в стержне, выдаются усилия на всё сечение колонны (раздельно N, M, Q), без учета совместного влияния момента в плоскости пилона на значение сжимающей силы), а при пластинчатом моделировании усилия выводятся в каждом конечном элементе отдельно (растягивающее и сжимающее напряжение на торцах пилона отличаются из-за влияния момента в плоскости пилона, а также кручения) и пользоваться ими неудобно, так как приходится вручную собирать усилия по всем конечным элементам пилона, чтобы получить, например, вертикальную силу N или момент M, для последующей проверки сечения в другой программе. Стержневой элемент показывает общее (собранное) усилие, а пластинчатый — кусочно распределенные, поэтому, чтобы в пластинчатом элементе получить привычные усилия, нужно вручную их собрать по всем конечным элементам пилона (по ширине — в плоскости пилона и по высоте — из плоскости пилона), распределение напряжений по сечению для стержневых элементов (в упругой стадии работы элемента) принимается по формулам сопромата. В пластинчатом пилоне удобнее смотреть характер распределения напряжений по его ширине, с учетом смещений вышележащих пилонов, а также можно увидеть зону концентрации напряжений, при изменении сечения вышележащего пилона (и его смещении вдоль нижележащего, более длинного пилона). Стержневыми пилонами удобнее пользоваться при выполнении расчета продавливание плит по замкнутому контуру. С пластинчатых пилонов сложно корректно собрать моменты в двух плоскостях, но продавливание на торце пилона удобнее проверять при моделировании пилона пластинами, так как в этом расчете нужно знать момент из плоскости пилона возле зоны продавливания, а он берется не со всего пилона, а с той части, которая примыкает к зоне продавливания (возле торца пилона).
При моделировании пилонов пластинами, значение максимального момента и поперечной силы в плите (в зоне примыкания к пилону) рассчитывается не для одного узла, в котором стержень соединяется с плитой, а распределяется в соответствии с заданным сечением пилона и область верхнего армирования становится шире, по сравнению со стержневым заданием пилона. Соответственно и зона армирования (точка теоретического обрыва арматуры) смещается. Поэтому моменты и поперечные силы в плите перекрытия могут заметно отличаться (по величине и конфигурации в плане) у прямоугольных пилонов смоделированных стержнями, по сравнению с пластинчатыми. Поэтому, при моделировании пилонов стержнями, нужно делать АЖТ в плитах перекрытий, учитывающих конфигурацию сечения пилона. Следует также отметить, что пластинчатые пилоны (в зависимости от своего расположения в расчетной схеме) могут собирать на себя немного больше вертикальной нагрузки, по сравнению со стержневыми без АЖТ (из-за включения в работу большей площади перекрытия). При подборе арматуры нужно помнить, что расчет арматуры в пластинах и стержнях, в программе, может отличаться (так как есть отличии в формулах СП для стен (плоскостных элементов) и колонн (стержневых элементов)), поэтому, перед расчетом, следует подробно изучить документацию: как, в данной программе, учитывается сжимающая сила в стержнях и пластинах, проверяются ли средние напряжения в сечении стержня и пластины, по каким формулам производится проверка на действие поперечных сил, крутящих моментов, как задается (и учитывается в расчете) расчетная длина для пластинчатого пилона, как учитывается коэффициент продольного изгиба (для колонн он обычно учитывается в двух плоскостях стержня, а в пластинах — в одной плоскости, из плоскости стены, поэтому, при моделировании высоких и относительно узких пилонов пластинами, этот коэффициент не будет учитываться при изгибе пилона в его плоскости), не во всех расчетных программах есть возможность учета продольного изгиба для пластин, без учета продольного изгиба арматуры в пилоне будет заметно меньше (необходимость учета продольного изгиба в плоскости и из плоскости пилона также определяется расчетом его гибкости, гибкость стен в их плоскости небольшая, поэтому влиянием продольного изгиба в плоскости стен пренебрегают), если нет такой информации или есть сомнения в правильности расчета, то лучше провести проверки отдельно в подпрограммах, или вручную, для обоих вариантов. Расчет на продавливание перекрытий опирающиеся на торцы стен отличается от аналогичного расчета перекрытий, лежащих на колоннах (отличие в длине учитываемого в расчете расчетного контура продавливания), поэтому, если пилон больше похож на стену чем на колонну, продавливание нужно считать по методике для стен, а не для колонн.
Наружные стены подвалов, соединенные с перпендикулярными к ним пилонами корректнее рассчитывать, при моделировании пилонов пластинами, так как пластинчатые элементы, соединенные друг с другом, более корректно передают усилия друг на друга и на плиты. Однако, в местах перехода пластинчатого пилона на стержневой (обычно в уровне плиты перекрытия над подвалом) возникает концентрация напряжений, в плите, возле стержня колонны (соединенного с пластинчатым пилоном внизу, под перекрытием), чтобы этого избежать, можно сделать АЖТ в данном стыке (в плите перекрытия), но лучше сделать два расчета, сначала смоделировать пилон на первом, втором этаже и в подвале пластинами, а потом стержнями (с АЖТ). В первом случае моделирование будет более корректным, так как в подвале пилон из пластин соединится с наружной стеной и плитой первого этажа, а дальше продлиться до второго и третьего, при этом будет отсутствовать концентрация напряжений в месте соединения стержня с пластинами, что даст корректную картину распределения напряжений. Однако, коэффициент продольного изгиба для пластин учитывается не во всех программах, поэтому, для контроля, можно задать пилоны стержнями и проконтролировать армирование.
Также стоит отметить, что моделирование пилонов пластинами занимает гораздо больше времени чем стержнями и результаты расчета зависят от размера конечных элементов, на которые разбивается пилон (особенно в верхней и нижней трети полона), поэтому при создании расчетной схемы на стадии «П» пилоны и колонны удобнее моделировать стержнями (с АЖТ), это позволяет быстро проанализировать усилия во всем здании и, при необходимости, быстро изменить сечения. Каркас сооружения при этом будет немного податливее чем при моделировании пилонов пластинами, но при нахождении общих перемещений и ускорений здания это упрощение будет в запас, поэтому допустимо. При моделировании пластинами нагрузка действует по разному на разные стороны пилона, если есть какие-то сосредоточенные или распределенные нагрузки с одной из сторон пилона, эта нагрузка будет больше нагружать одну из сторон пилона и будет проявляться эффект местного приложения нагрузки. В квадратных колоннах и пилонах с отношением сторон более 1/2 такой эффект практически отсутствует.
Про пилоны с промежуточными габаритами сечений написано в СП 63.13330.2018, в пункте 10.4.6. Там говорится о том, что армирование пилонов, занимающих по своим геометрическим характеристикам промежуточное положение между стенами и колоннами, производят как для колонн или как для стен в зависимости от соотношения длины и ширины поперечного сечения пилонов. Тут нужно обратить внимание на то, что в этом пункте не сказано о расчете, а только об армировании, т. е. этот пункт является продолжением пунктов 10.4.2 и 10.4.3, в которых описываются общие требования к армированию колонн и стен. Тем не менее, в СП 63, для стен есть конкретные формулы, отличные от расчета колонн (как стержневых элементов), в частности, в пункте 8.1.57 приводятся формулы для расчета стен с учетом сил, действующих по боковым сторонам плоского выделенного элемента. Пример усилий на плоском (пластинчатом) элементе показаны на рисунке 8.16 СП 63. Этими формулами можно пользоваться только при моделировании пилона пластинами, поэтому, если пилон по своим геометрическим характеристикам относится к стенам, то его прочность логично рассчитывать по формулам для стен, а ими можно пользоваться, только при моделировании пилона пластинами.
Следует помнить что «стыки колонн с гладкой плитой (без капителей) или балкой являются условно жесткими», поэтому расчетную длину таких колонн следует определять в запас. При наличии капители у пилона его лучше моделировать пластинами, так как капители принято моделировать утолщенными пластинами с эксцентриситетами (вниз или вверх), а при моделировании пилона стержнем, в плите делают АЖТ, поэтому при наложении эксцентриситетов (капители) с АЖТ (которое делают для соединения стержня с пластинами капители) могут быть некорректные результаты при расчете усилий.
Помимо отличий в расчете и армировании есть еще и конструктивное отличие, о котором говорится в пункте 10.2.2 СП 63: «Размеры сечений внецентренно сжатых элементов для обеспечения их жесткости следует принимать такими, чтобы их гибкость в любом направлении не превышала: 200 — для железобетонных элементов (включая стены); 120 — для колонн, являющихся элементами зданий; 90 — для бетонных элементов». Т. е. если пилон относится к стенам, то его гибкость не должна превышать 200, а если к колоннам, то 120.
Следует помнить и о том, что в пилоне смоделированный пластинами горизонтальная арматура (хомуты) будет подбираться с расчетным сопротивлением продольной арматуры (вертикальной и горизонтальной), а не поперечной. Например, если в качестве хомутов будет использоваться арматура А500С, то при расчете хомутов по первому предельному состоянию расчетное сопротивление следует брать 300 МПа, а не 435 МПа, но в пластинах, для обои направлений программа примет одинаковое расчетное сопротивление, т. е. 435 МПа для арматуры А500С, таким образом, площадь горизонтальной арматуры в пластинах (хомутов) нужно умножать на коэффициент больше единицы, чтобы учесть уменьшение расчетного сопротивления для поперечной арматуры.
Пункт 7.1.8 СП 63.1330.2018 требует учитывать влияние продольного изгиба для железобетонных элементов с гибкостью более 14. Так для внутренних пилонов здания, при высоте этажа (в свету) 3 м и расчетной длине l0 = 3 х 0,85 = 2,55 м, максимальная длина сечения, при которой, по аналогии со стеной, можно не учитывать влияние продольного изгиба в плоскости пилона, будет l0 / i = 630 мм. При стороне пилона больше 630 мм нужно учитывать коэффициент продольного изгиба в плоскости пилона. Указанное в пункте 5.1.8 СП 430 значение hэт / b > 3, где hэт — высота этажа в свету, а b — наибольший размер поперечного сечения пилона дает результат 300 / 63 = 4,76, что больше 3, т. е. колонна может стать стеной только при стороне сечения большей 300 / 3 = 100 см (и второй стороне сечения менее 100 / 4 = 25 см). Таким образом, при указанной высоте и большей стороне сечения, находящейся в интервале 630 — 1000 мм колонна является пилоном, при расчете которого СП 63 допускает не учитывать коэффициент продольного изгиба в плоскости пилона, но при этом, в соответствии с СП 430, данный пилон не является стеной. О том, какое же тогда отличие между пилоном и стеной СП 430 умалчивает. В СП 63 тоже не сказано, при каких соотношениях пилон считать стеной. В списке нормативных ссылок, в СП 63, на другие нормативные документы СП 430 отсутствует, поэтому разделение на стены, пилоны и колонны читателю придется делать самому, однако, в приложении «В», в пункте В21, авторы норм пишут следующее: «При построении конечно-элементной расчетной модели размеры и конфигурацию конечных элементов следует задавать, исходя из возможностей применяемых конкретных расчетных программ, и принимать такими, чтобы была обеспечена необходимая точность определения усилий по длине колонн и по площади плит перекрытий, фундаментов и стен«. Т. е. инженер должен сам выбрать наиболее оптимальную модель, с помощью которой будет определяться напряженно-деформированное состояние в элементе. Например, при отсутствии в программе возможности учета продольного изгиба из плоскости стены для пластинчатых (или оболочечных) конечных элементов — моделировать стены стержнями или собирать усилия с пластин вручную, и считать стену в другой программе, которая предоставляет возможность учесть все факторы, влияющие на подбор арматуры. Так как данная процедура отнимает много времени и ни каждый ей владеет большинство моделирует пилоны стержневыми конечными элементами с жесткими телами в плитах, или с пластинами повышенной жесткости в габаритах сечения пилона.
На простом примере можно наглядно убедиться, что распределение нормальных напряжений в сечении пилона, смоделированного пластинами и стержнем — отличается. При моделировании стержнем момент в заделке постоянный и не зависит от габаритов сечения пилона, зависит только от его высоты, а распределение нормальных напряжений в опорном сечении (при проверке прочности и подборе арматуры) принимается линейным или меняется, в зависимости от принятой диаграммы арматуры и бетона (при расчете сечения по нелинейной деформационной модели), а также величины момента.
Ниже приведены результаты расчета пилона высотой 3 м и толщиной 200 мм, нагруженного горизонтальной силой 3.33 тс, при моделировании пластинами и стержнем (при обычном, упругом, расчете). Длина сечения меняется от 400 мм до 27 метров. Отличие в напряжениях на торце пилона тем больше, чем меньше отношение длины сечения к высоте пилона. При отношении высоты пилона к длине сечения меньше 1 распределение нормальных напряжений в нормальных сечениях пилона перестает быть равномерным, почти на всей высоте пилона, гипотеза плоских сечений не выполняется также, почти на всей высоте пилона и при уменьшении этого отношения перестает работать вообще. При таких соотношения моделирование пилона (стены) стержнем приведет к большим неточностям расчета, которые могут привести к печальным последствиям.
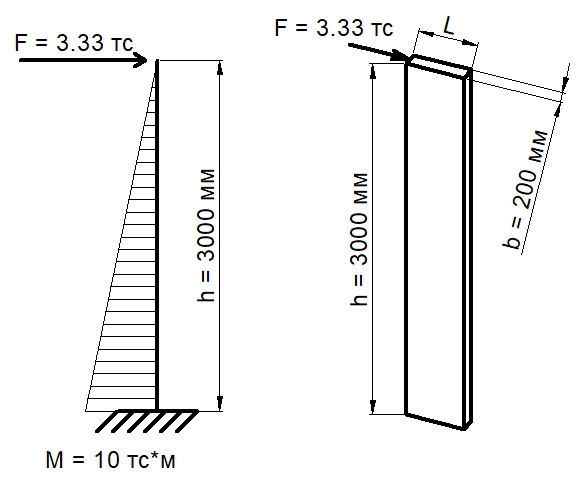
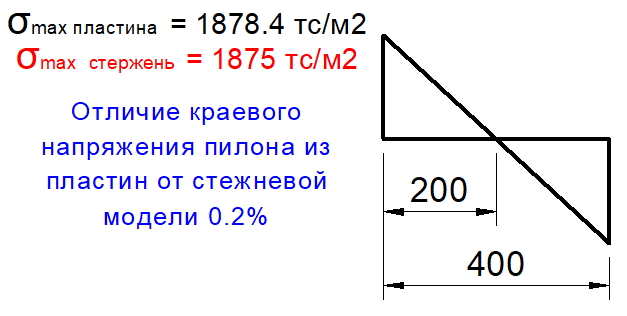

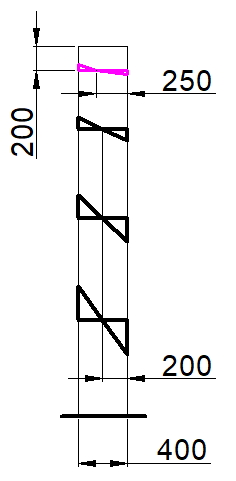
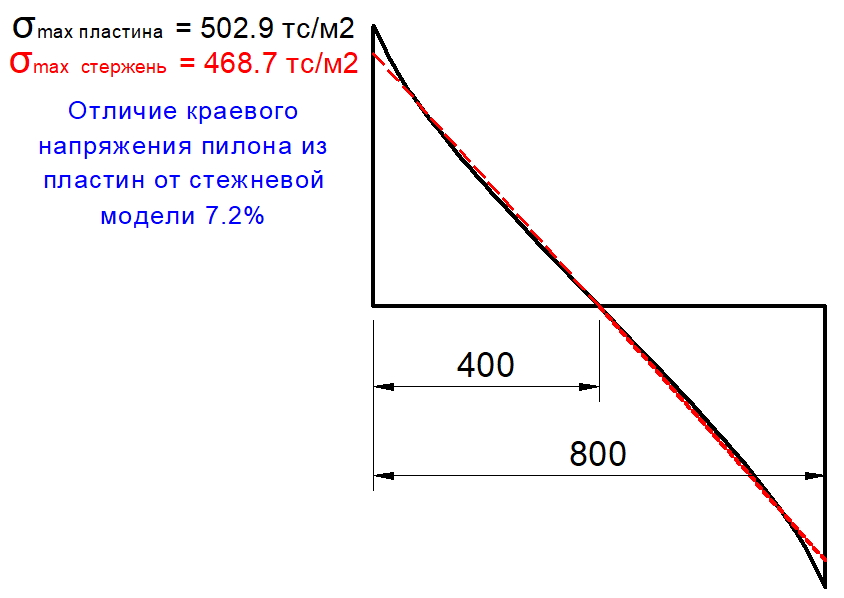
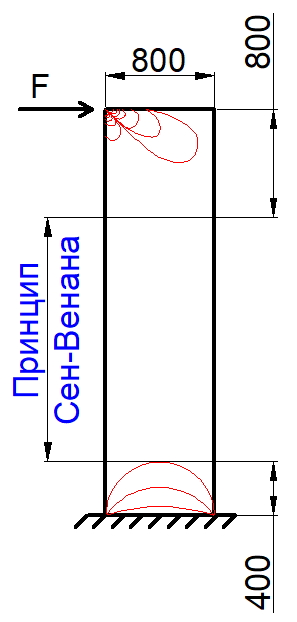
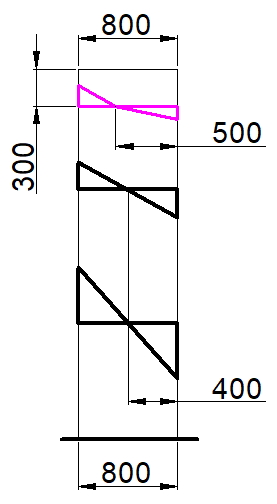
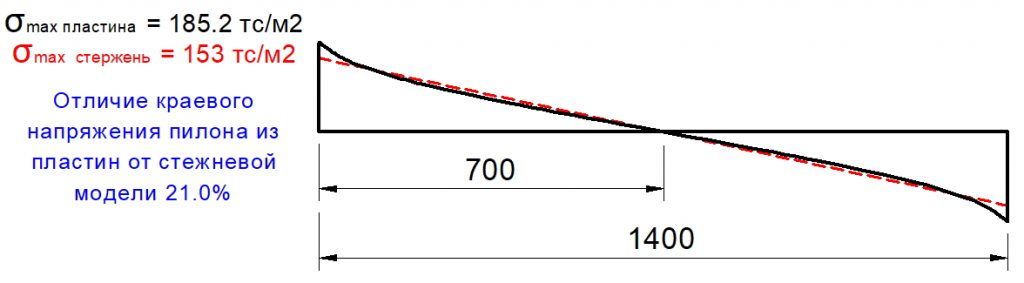
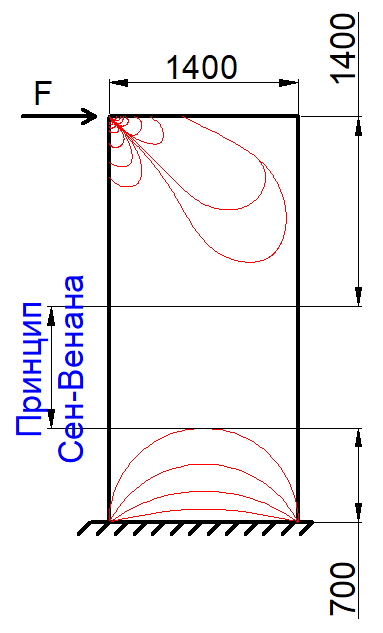
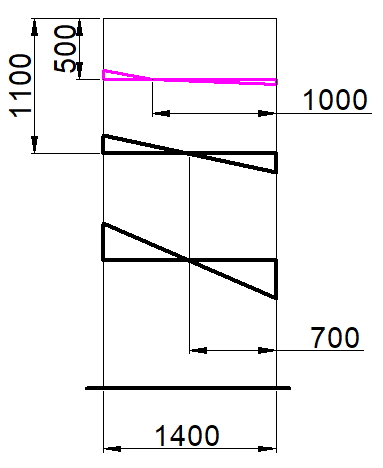
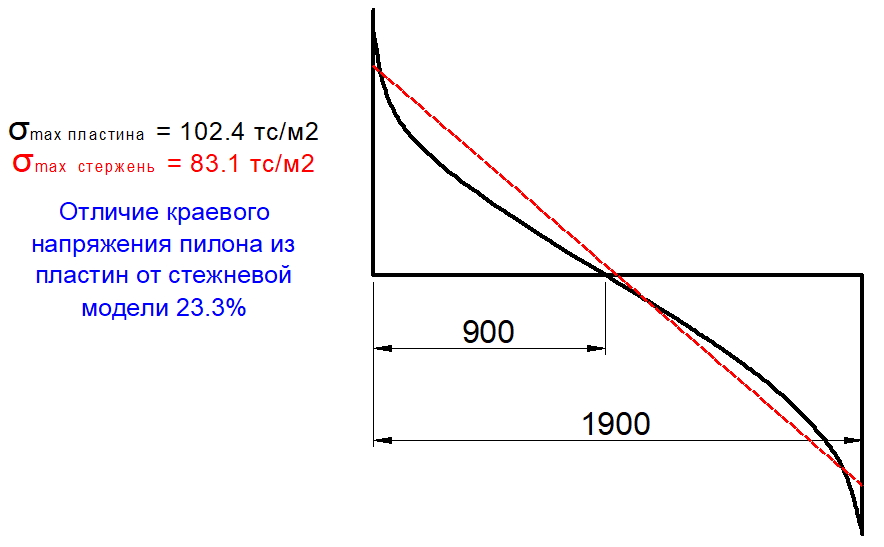
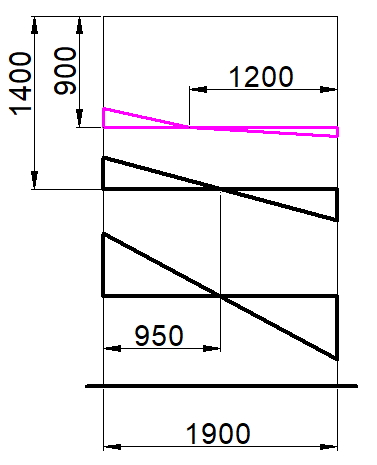
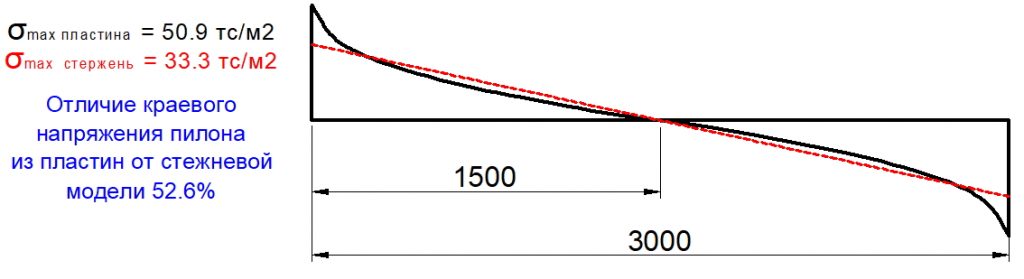
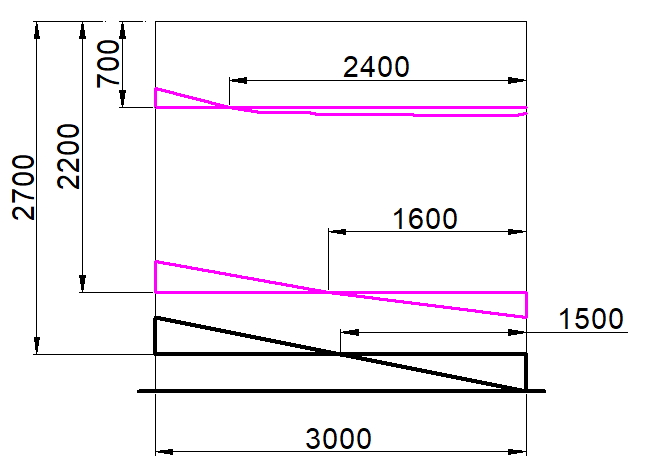

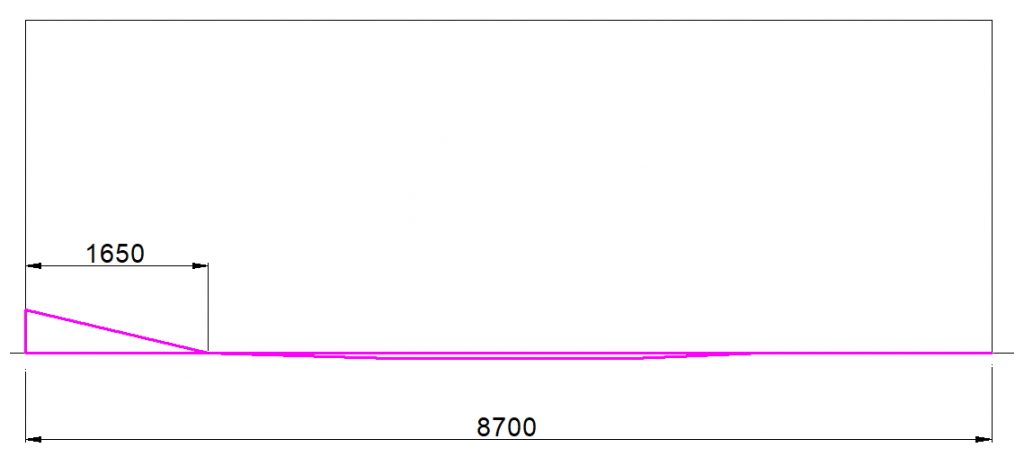

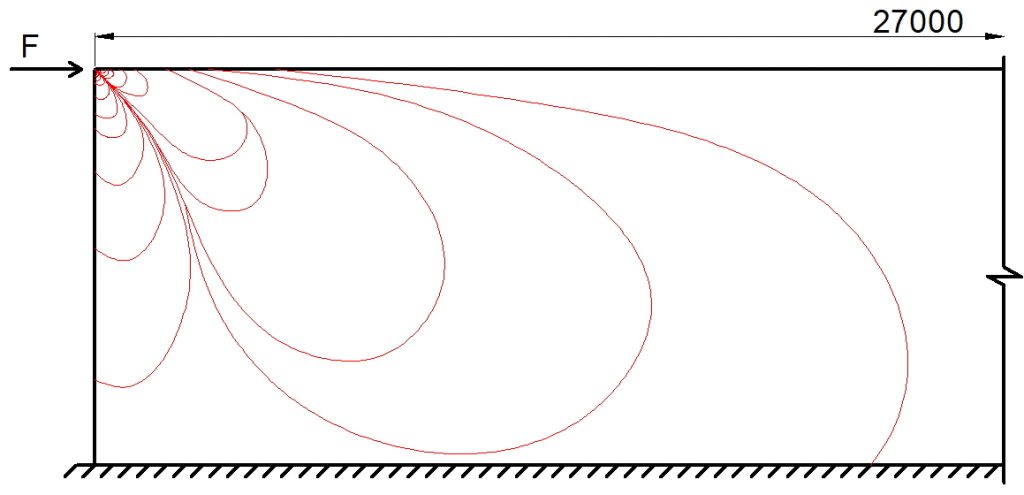
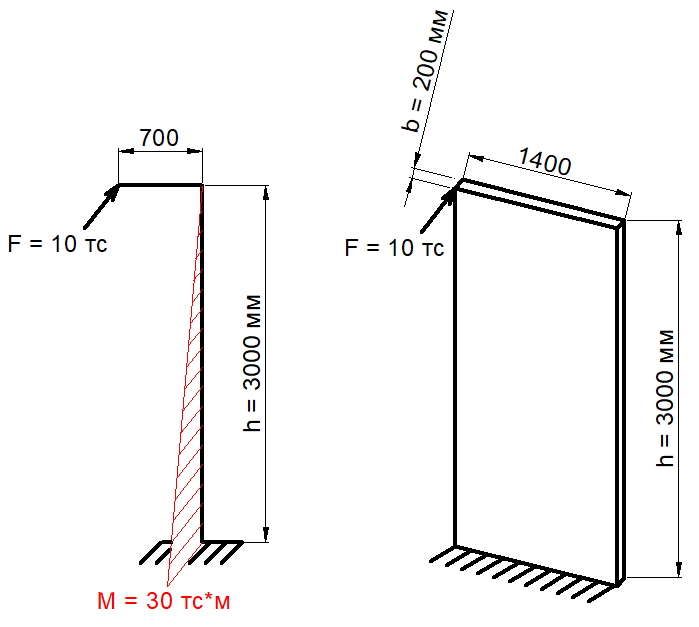
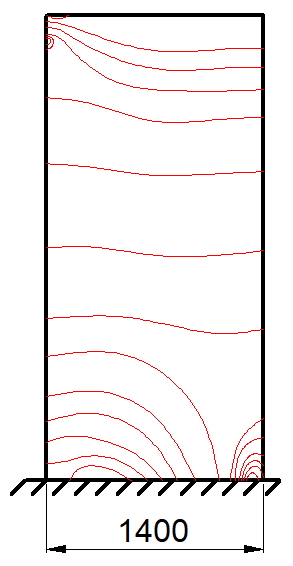
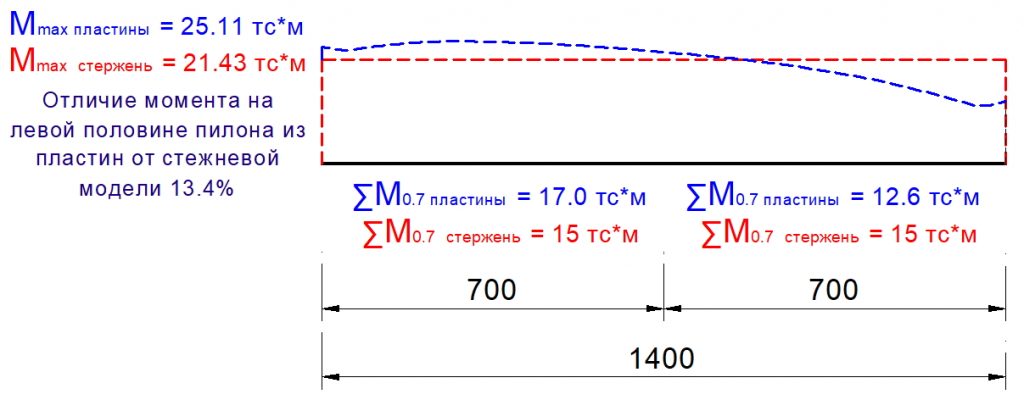
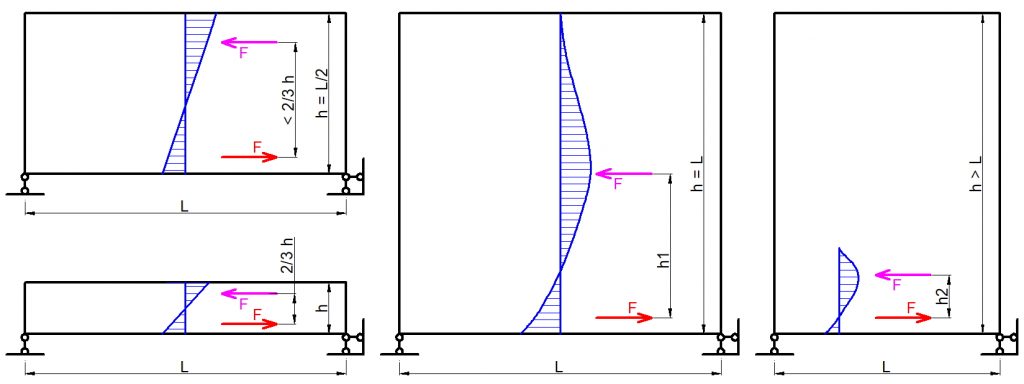
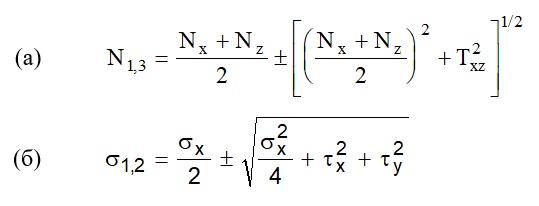
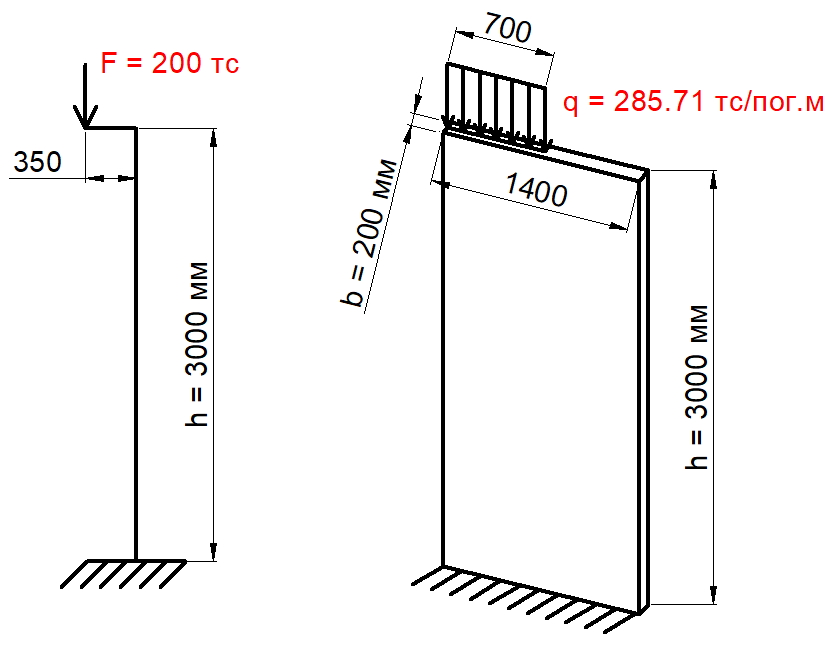
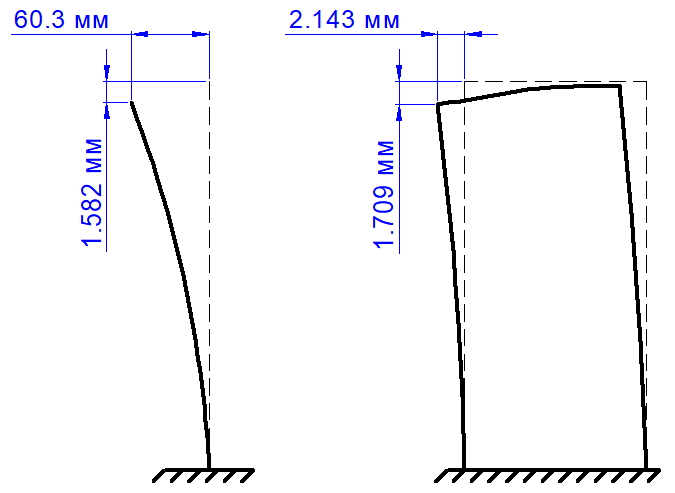
Об отличиях работы стен на горизонтальную нагрузку (ветровое воздействие или сейсмику) от стержневых элементов также писали многие авторы и в нашей стране, и за рубежом. В качестве примера можно процитировать, например, статью С. Б. Смирнова (БиЖ, 2001 г., №6) «Расчет прочности железобетонных стен и диафрагм методом однородных полей»: «Отличие работы стен от работы коротких и длинных консольных балок заключается в том, что горизонтальные сейсмические нагрузки Q передаются от дисков перекрытий на стены в виде касательных напряжений распределенных по верхней грани стены (диафрагмы). Такие нагрузки создают большие зоны интенсивного сдвига (положительных и отрицательных главных напряжений), что требует дисперсного армирования… Диски перекрытий являются упругими плавающими заделками для стен и создают частичное защемление ячеек стены». При моделировании стержнем такие зоны и величины напряжений определить очень сложно, поэтому в зданиях, которые рассчитываются на сейсмическую нагрузку пилоны с отношением сторон сечения 1/4 — 1/6 и менее должны моделироваться пластинами, чтобы корректно определить главные и касательные напряжения. В зданиях до 40 м, на которые ветровая нагрузка, практически, не оказывает влияния и вертикальные усилия в пилонах небольшие, можно, для упрощения анализа расчетной схемы, их моделировать стержнями. В любом случае габариты колонн (пилонов) нужно стараться назначать такими, чтобы для них можно было применять классические методики расчета стержневых элементов, так как полной, точной, всеобъемлющей (исчерпывающей) методики расчета стен смоделированных пластинами (или оболочками) на сегодняшний день нет, поэтому ответственность за расчет и проектирование таких элементов (например, коробчатых сечений монолитных ядер жесткости, ж/б диафрагм жесткости неправильного сечения и др.) лежит на конструкторе. Если сечение пилона, по каким-либо соображениям, нельзя изменить до соотношения менее 1/4, то расчет лучше делать для двух вариантов: 1) при моделировании пилона стержнем; 2) при моделировании пилона пластинами (оболочками). Армировать по худшему из результатов. Это займет больше времени, но поможет избежать ошибок, связанных с особенностями каждой из методик.
В конечном счете, решение о том, как моделировать пилоны принимает конструктор (или расчетчик), на сегодняшний день, строгих предписаний по данному вопросу, в нормах (обязательных для применения в России), нет. В качестве рекомендаций можно посоветовать делать 2 расчетные схемы, одну с пилонами смоделированными стержнями, а другую — пластинами. При моделировании колонн стержнями, в местах примыкания стержней к плитам перекрытий, делать АЖТ, учитывающие конфигурацию колонны (пилона) и увеличивающие моменты, однако, расчетную длину можно (в запас) считать, как при шарнирном соединении с коэффициентом 1, для внутренних пилонов и 1.2 для наружных пилонов (по пункту 8.1.17 СП 63). Если отношение сторон сечения (большей стороны к меньшей) более 5, то данный пилон нужно относить к стенам и считать, как стену, смоделированную пластинами. При этом рекомендуется пластины разбивать промежуточными узлами так, чтобы шаг разбиения по длине стены был не более толщины стены и имел не менее трех промежуточных узлов по длине сечения стены. По высоте шаг разбиения принимают таким, чтобы получались конечные элементы квадратного сечения после разбиения вдоль сечения стены. Т. е. длина и высота каждого конечного элемента были одинаковыми. В середине высоты пилона можно делать прямоугольные конечные элементы. Обязательным также является наличие промежуточного узла ровно в середине длины сечения.
5. Об особенностях расчета на продавливание при различных видах моделирования колонн;
6. Статья об осреднении поперечной арматуры в зоне продавливания;
8. Статья «Моделирование перемычек, простенков, пилонов» в программе ЛИРА-САПР.
Плитный фундамент на естественном основании
Проектирование плитных фундаментов (ПФ) начинается с определения их толщины и размеров (при условии, что глубина заложения известна). Общая толщина ПФ назначается в зависимости от конструктивной схемы здания, количества этажей и типа грунтов под подошвой. Очень часто, при совмещенной (каркасной) конструктивной схеме здания (колонны со стенами) делают местные утолщения ПФ под колоннами, для исключения продавливания. Продавливание считают от расчетных нагрузок с учетом понижающих коэффициентов (зависящих от количества этажей) и отпора грунта под пирамидой продавливания, располагающейся по угол 45 град. от граней колонны к основанию (отпор рекомендуется учитывать с коэффициентом 0,5). Отпор грунта (среднее давление), при расчете продавливания, считают от расчетных нагрузок. Продавливание проверяют без учета поперечного армирования. Толщину ПФ, в местах расположения монолитных стен, проверяют по прочности наклонных сечение (на действие силы Q), также без учета поперечной арматуры. В плане ПФ разделяют деформационными швами в случае, если их размеры больше указанных в таблице… СП… Данные швы устраивают при разной высотности зданий стоящих на одной плите, для того, чтобы избежать большой концентрации усилий в зоне перепада высот, такие швы называют осадочными деформационными швами. Также деформационные швы устраивают при большой протяженности ПФ для того, чтобы избежать температурных напряжений (температурные деформационные швы), однако, если произвести температурный расчет плиты и заложить необходимое по расчету дополнительное армирование, температурные швы можно не делать.
Рекомендуемые параметры жесткости основания для расчета верхней и нижней арматуры плитного фундамента описаны в СП 50-101-2004 в пункте 12.5.5: «Рекомендуется выбирать наиболее неблагоприятные значения параметров жесткости основания и модели основания для каждого расчета (в частности, расчет сечения верхней арматуры производить при постоянном коэффициенте постели, а нижней — при переменном)». При моделировании основания объемными элементами данный пункт СП рекомендует моделировать основание так, чтобы объемные элементы находились только под площадью плиты и не выходили за пределы фундамента.
Требования к вертикальным перемещениям плитных фундаментов
Для нескальных грунтов расчет оснований по деформациям является обязательным для всех типов зданий и сооружений. Величины допускаемых предельных вертикальных деформаций основания для фундаментов объектов нового строительства указаны в таблице Г.1 СП 22.13330.2016. Данные величины были получены из опыта многолетних экспериментов, а также наблюдений за существующими зданиями и сооружениями. К примеру, для железобетонных зданий с полным каркасом значение максимально допустимой (или средней) осадки, за прошедшие 50 с лишним лет, увеличилось с 10 см (СНиП II-Б.1-62) до 15 см (СП 22.13330.2016). Значение допускаемых максимальных вертикальных перемещений, при необходимости (технологической, функциональной или др.), можно уменьшить, для этого уменьшенное значение необходимо указать в задании на проектирование.
Средней осадкой считается среднее значение осадки среди минимум трех точек (по значением трех скважин) плитного фундамента или минимум трех абсолютных значений осадок столбчатых фундаментов, объединенных общей конструкцией. Максимальной считается осадка отдельно стоящего столбчатого фундамента или жесткого центрально нагруженного плитного фундамента.
Среднее давление под подошвой центрально нагруженного фундамента определяют отношением суммарной нормативной нагрузки от основного расчетного сочетания к площади фундамента. Это давление не должно превышать расчетное сопротивление грунта.
При расчете осадки необходимо учитывать факторы влияющие на неравномерность осадки. К неравномерной осадке и крену приводит внецентренное приложение суммарной нагрузки от веса здания, а также близкое расположение соседних зданий (и очередность их возведения). Если рядом со строящимся зданием отсутствуют соседние здания (или сооружения), но есть неслежавшиеся насыпи (насыпные грунты), которые продолжают уплотняться, их следует учитывать в виде дополнительной нагрузки на основание. Деформации основания от насыпей учитывают и до строительства здания и после. При неравномерной высоте и расположении, такие насыпи могут привести (со временем) к неравномерной осадке или крену возведенного здания. Следует помнить, что уплотнение насыпных грунтов, в зависимости от их состава и способа образования насыпи может длиться 0,5…30 лет. Еще одним фактором, приводящим к неравномерной осадке основания и крену, является наличие, под фундаментом, грунтов с разными характеристиками сжимаемости, поэтому, для плитных фундаментов, необходимо определять осадку минимум по трем скважинам, расположенным в разных точках плиты.
Общие проверки расчета по деформациям наиболее полно описаны в Пособии по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83). Для расчета деформаций пользуются основным расчетным сочетанием нагрузок с коэффициентами надежности по нагрузке равными 1, в которое входят постоянные, длительные и кратковременные нагрузки. Длительными считают кратковременные нагрузки от веса людей и снега с коэффициентами длительности 0,35 и 0,5 соответственно. Пульсационную составляющую ветра при расчете осадок не учитывают, так как считается, что при кратковременных динамических нагрузках основание работает упруго и длительная часть осадки проявиться не успевает. Ветровую нагрузку учитывают при проверке максимального давления вдоль края фундамента и в его углах, а при расчете средней (или максимальной) осадки эту нагрузку можно не учитывать, так как направление ветра со временем может меняться и точно учесть добавочную величину осадки именно от ветра, в суммарной осадке, которая рассчитывается из общего срока эксплуатации здания крайне сложно. При проверке разности осадок, прогиба и выгиба фундамента рекомендуется пользоваться пониженными модулями бетона, см. формулу 6.3 СП 63.13330.
Ссылки:
Большинство расчетных программ выдает результаты посчитанных усилий на 1 погонный метр. Это связано с тем, что нагрузки также задаются на 1 м2 (или 1 пог.м).
Например, в результате расчета стены или пилона, который смоделирован пластинчатыми элементами нужно определить значение сжимающей силы N. Для этого нужно отобразить вертикальные напряжения Ny (или Ss в программе ing+) в пластинах, далее нужно собрать данное распределенное усилие в одну силу, т.е. нужно умножить усилие Ny (в Т/м2) действующее вдоль пластины на толщину пластины (м) и на ширину пластины (расстояние между её крайними узлами по ширине), перпендикулярно направлению данного усилия. Таким образом можно узнать сосредоточенную силу в конкретном пластинчатом элементе пилона или стены. Чтобы узнать общую сосредоточенную продольную силу N, в пилоне, а не в конкретном конечном элементе, нужно просуммировать полученные сосредоточенные силы, полученные в каждой пластине пилона, в одном ряду (по всей ширине пилона, вдоль одной линии). Удобнее всего находить данное усилие в среднем ряду пилона (в средней части высоты пилона), в этих местах меньше сказываются эффекты точечного приложения сил и картина усилий равномерная.
Чтобы определить момент в сечении пилона (с учетом действия сжимающей силы N), полученные при определении общей сжимающей силы в пилоне значения сосредоточенных сжимающих сил по каждому конечному элементу, нужно умножить на соответствующие расстояния до точки нулевого напряжения в сечении. Получив таким образом значения моментов их нужно просуммировать в соответствии со своими знаками. В итоге получится суммарный момент в данном сечении пилона, с учетом действия сжимающей силы N.
Так как усилия в узлах определяются через перемещения, для получения более точного результата, пластинчатый элемент пилона нужно поделить минимум на четыре конечных элемента по ширине и, принимая высоту конечных элементов равной ширине, на соответствующее их количество по высоте пилона.
Рис. 1. Определение момента в плоскости пилона при стержневом и пластинчатом моделировании
Рис. 2. Определение момента из плоскости пилона при стержневом и пластинчатом моделировании
Рис. 3. Определение сжимающей силы N при стержневом и пластинчатом моделировании
Рис. 4. Определение момента M в опорном сечении при одновременном действии сжимающей силы и момента в плоскости пилона
Рис. 5. Определение крутящего момента T в сечении по величине касательного усилия в срединной плоскости оболочки.
Коэффициенты альфа и гамма можно приведены в таблице ниже.
Ссылки
Короткие ж/б элементы часто применяются в монолитных и сборных зданиях и сооружениях. В [1] и [2] приводится перечень элементов, которые можно отнести к классу коротких: «Класс коротких элементов составляют консоли колонн, опорные консоли ригелей с подрезками, короткие балки и их разновидности. Сюда также могут быть отнесены монолитные узлы сопряжений и участки конструкций, в которых реализуется принцип работы коротких элементов. К ним относятся монолитные узлы соединения ригелей с колоннами; приопорные участки балок L/h не превышает единицы; ростверки свайных фундаментов при ленточном нагружении, а также диафрагмы жесткости при совместном действии вертикальных и горизонтальных сил… Приопорные участки обычных балок при нагружении сосредоточенной силой, расположенном на небольшом расстоянии от опоры, т.е. при значении L/h, близком к единице, также по характеру работы подобны коротким элементам. Короткие плиты, некоторые виды фундаментов, по своей работе не имеют сколько-нибудь значительных отличий от коротких элементов [1]», «…ростверки свайных фундаментов под стеновые конструкции при двухрядном расположении свай, при шахматном расположении свай, ростверки свайных фундаментов под колонны с многорядным расположением свай, узлы сопряжения колонн с продольными и поперечными балками в монолитных каркасах зданий и сооружений, фундаменты под колонны, капители колонн безбалочных перекрытий и др. …Более емким, простым и характерным определением перечисленных конструкций является понятие «толстые плиты»… [2]».
Рис. 1. Железобетонные элементы, работающие в продольном и поперечном направлениях при малом пролете среза, относящиеся к классу коротких ([2])
Отличие в работе ж/б коротких элементах было замечено более 100 лет назад. Тогда и была придумана каркасно-стержневая методика расчета.
Ферменно-стержневой (каркасно-стержневой) метод расчета наклонных сечений балок был придуман независимо друг от друга двумя инженерами, в 1899 году швейцарским инженером Риттером и в 1902 году немецким инженером Мёршем, поэтому впоследствии, название закрепилось, как метод Риттера-Мёрша. Суть метода состоит в представлении ж/б элемента в виде фермы с шарнирными узлами, состоящей из стоек и раскосов (стяжек).
В СССР данным вопросом подробно занималась Тамара Ивановна Баранова, которая написала много статей, посвященных данной теме и стала соавтором кандидатских диссертаций, которые, впоследствии, были приняты для разработки Норм по проектированию бетонных и железобетонных конструкций.
Основные отличии
Отличий в работе коротких ж/б элементов от длинных несколько, их подробно описывает Тамара Ивановна в своей книге «Каркасно-стержневые расчетные модели и инженерные методы расчета железобетонных конструкций»: «В значительной степени напряженно-деформированное состояние коротких элементов определяется местными напряжениями, влияющими на характер распределения напряжений и деформаций. Сближение зон местных напряжений, благодаря малым габаритам коротких элементов, согласно принципу Сен-Венана, оказывает существенное влияние на сопротивление, в то время как в обычных конструкциях местные напряжения играют второстепенную роль.
По сравнению с обычными (длинными) элементами характер распределения нормальных напряжений в коротких элементах изменяется в значительной степени. В сечениях конструкций коротких элементов, в которых нормальные напряжения равны нулю, распределение главных сжимающих напряжений не соответствует распределению касательных напряжений, имеющему место в обычных конструкциях, поэтому нейтральная ось в коротких элементах утрачивает свое значение.
Касательные напряжения имеют отличный от параболического очертания характер распределения и являются незначительными по величине. Можно предположить, что их роль существенно сказывается лишь при определении величины и направления главных напряжений: сжимающие и растягивающие нормальные напряжения, касательные напряжения, а также местные напряжения при сближении зон их влияния. В результате возникает сложное напряженное состояние.
Решающую роль в коротких элементах играют главные напряжения, интенсивность распределения которых отличается концентрацией, усугубляющейся геометрическими очертаниями и видами нагружения. Как правило, главные растягивающие и сжимающие напряжения сосредотачиваются в потоки. Подтверждением этому является известная ферменная аналогия Мёрша, широко используемая для коротких элементов в зарубежной практике».
Виды разрушения коротких элементов
В [1] приводятся следующие результаты наблюдений: «Как показывают исследования, в коротких консолях при действии сосредоточенных сил сначала образуются трещины в бетоне опорного сечения. По своему характеру эти трещины приближаются к нормальным трещинам изгибаемых элементов, однако их траектории в зависимости от ряда причин отклоняются вглубь колонны, оставаясь перпендикулярными к направлению главных растягивающих напряжений. Длина и ширина трещин зависит от количества продольной арматуры.
Кроме того, в средней части консоли образуются наклонные трещины, природа которых недостаточно изучена…
Образование трещин определяет два вида разрушения. Первый вид характеризуется развитием трещин в опорном сечении консоли, т.е. в зоне растяжения…
Второй вид представляет собой разрушение бетона в результате сжатия по направлению от действия силы к опоре, т.е. в пределах высоты короткого элемента… Рассмотренный вид разрушения является особенностью коротких элементов…
Влияние отношения расстояния (а) приложения силы относительно оси опоры и высоты элемента (h0) а/h0 изучалось многими авторами…
Следует обратить внимание на тот факт, что с увеличением величины a/h0 наблюдалось изменение вида разрушения коротких элементов. Как правило, при a/h0, равном 0.1-0.7, разрушение происходило по сжатой полосе бетона, при a/h0, равном 0.7-1.0, наступал переход к разрушению по растянутому поясу (или смешанный вид разрушения)…
Обобщая картину образования и развития трещин, можно выявить, что в коротких элементах существует три вида трещин, два из которых являются основными. Назовем их в порядке образования. Это трещины в растянутой зоне (обозначим их величиной Т-Р), образующиеся у растянутой грани элемента, и основные наклонные трещины (обозначим их величиной Т-О), образующиеся при более высоком уровне нагружения в наклонных сжатых участках бетона, расположенных между грузовой и опорными площадками. К третьему виду относятся трещины, обозначим их величиной (Т-Г), проходящие по границе между растянутой и сжатой зонами, а также трещины, выделяющие наиболее напряженный наклонный участок с внешней стороны».
Рис. 2. Схема расположения характерных трещин в коротких элементах: а — консоли колонны, б — приопорные участки ригелей с подрезками, в — короткие балки (балки-стенки).
Рис. 3. Характер и виды разрушений коротких ж/б элементов: а — коротких консолей; б, в — приопорных участков ригелей с подрезками; г — коротких балок (балок стенок); д — диафрагм жесткости при совместном действии горизонтальных и вертикальных сил; е — ростверков свайных фундаментов при ленточном нагружении; ж — жестких узлов.
Рис. 4. Траектории главных напряжений: а — в консолях колонн; б — в опорных консолях ригелей; в — в коротких балках; г — в подкрановых ригелях колонн; д — в перемычках колонн.
Рис. 5. Колонна с короткими консолями после испытаний
Рис. 6. Каркасно-стержневая модель (SP-208)
Рис. 7. Схема распределения трещин в балке после испытаний
Рис. 8. Каркасно-стержневая модель (SP-208)
Рис. 9. Испытание балки-стенки при действии равномерной нагрузки (SP-208)
Рис. 10. Каркасно-стержневая модель (SP-208)
Рис. 11. Испытание балки-стенки таврового сечения при действии равномерной нагрузки приложенной к нижнему поясу (SP-208)
Рис. 12. Каркасно-стержневая модель (SP-208)
Рис. 13. Испытание ригеля с подрезкой
Рис. 14. Каркасно-стержневая модель (SP-208)
Рис. 15. Один из натурных экспериментов для подтверждения каркасно-стержневой модели (с ресурса: https://www.istructe.org/fibuk/files/fib_bull45_nmg.pdf)
Рис. 16. Размеры испытанных в [2] ростверков
 Рис. 17. Характер трещинообразования и разрушения образца №1 из [2]
Рис. 17. Характер трещинообразования и разрушения образца №1 из [2]
 Рис. 18. Характер трещинообразования и разрушения образца №3 из [2]
Рис. 18. Характер трещинообразования и разрушения образца №3 из [2]
Рис. 19. Характер трещинообразования и разрушения образца №6 из [2]
В соответствии с СП63, п.5.2.1: «Расчет по прочности коротких железобетонных элементов (коротких консолей и других элементов) производят на основе каркасно-стержневой модели».
В Американских нормах ACI318R-14 данной модели расчета железобетонных элементов посвящена глава 23 («CHAPTER 23—STRUT-AND-TIE MODELS»). В ней приводятся примеры участков конструкций, которые необходимо рассчитывать по данной методике.
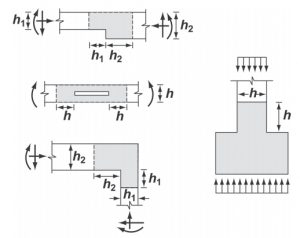 Рис. 20. Примеры конструктивных элементов, затененные участки которых необходимо рассчитывать по ферменно-стержневой аналогии. За этими зонами применяется общая теория расчета изгибаемых элементов по гипотезе плоских сечений.
Рис. 20. Примеры конструктивных элементов, затененные участки которых необходимо рассчитывать по ферменно-стержневой аналогии. За этими зонами применяется общая теория расчета изгибаемых элементов по гипотезе плоских сечений.
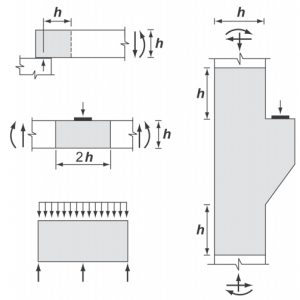 Рис. 21. Примеры конструктивных элементов, затененные участки которых необходимо рассчитывать по ферменно-стержневой аналогии. За этими зонами применяется общая теория расчета изгибаемых элементов по гипотезе плоских сечений.
Рис. 21. Примеры конструктивных элементов, затененные участки которых необходимо рассчитывать по ферменно-стержневой аналогии. За этими зонами применяется общая теория расчета изгибаемых элементов по гипотезе плоских сечений.
Моделирование балок-стенок в расчетных комплексах осуществляют не стержневыми, а пластинчатыми элементами. В некоторых программах данный тип конечных элементом так и называется «прямоугольный КЭ балки-стенки» или «назначение элемента — балка-стенка». В результате расчета необходимо получить усилия Nx, Ny (в перпендикулярных направлениях пластины) и Nxy, по которым подбирается армирование ж.б. конструкций или проверяется стенка металлической балки (если по устойчивости она проходит)…
В конце статьи хочется обратить внимание на особенности работы толстых фундаментных плит, которые особенно проявляются при небольшом отношении толщины плиты к пролету. Фрагмент текста из книги «Фундаменты» (авт. Тетиор А. Н.), глава 1.4: «В связи с большими нагрузками от зданий и сооружений конструкции фундаментов всех типов имеют большую толщину — от 30 см… до 3 м для фундаментов сооружений башенного типа. При таких размерах большую роль начинают играть усилия, действующие в плоскости плит, — мембранные силы, или силы распора, как следствие особенностей деформирования железобетона, главным образом существенно различающейся прочности при сжатии и растяжении. Следствием этого являются концентрированные потоки главных сжимающих напряжений, действующие в железобетонных плитах после образования и раскрытия трещин. Это ведет к возникновению значительных усилий распора, существенно меняющих напряженно-деформированное состояние элементов и приводящих к переходу от состояния изгиба к внецентренному сжатию.
Представление о действии концентрированных потоков главных сжимающих напряжений внутри фундаментных плит не только помогает более реально представить работу любой конструкции, но и позволяет в ряде случаев надежнее рассчитать ее прочность, рациональнее расположить рабочую арматуру. Условные концентрированные потоки главных (наибольших) сжимающих напряжений в железобетонных плитах идут от внешней нагрузки к опорам; при этом из рассмотрения исключается бетон, разделенный трещинами.
Оставшаяся часть сжатого бетона и образует условные полосы, или внутренние конструкции, которые воспринимают нагрузку. В связи с этим представляет интерес вопрос о траекториях трещин в бетоне.
Как известно, в хрупких телах (к которым можно отнести с некоторым приближением бетон) имеются три основных типа перемещения поверхностей трещин: нормальный отрыв, поперечный и продольный сдвиги…
Можно говорить только о приближении траектории трещин к траекториям главных напряжений — изостатам, так как гетерогенность структуры бетона и местные напряжения вблизи арматуры приводят к местным отклонениям траектории трещин от изостат, носящим как случайный характер (из-за наличия начальных дефектов и включений), так и силовой. В целом же трещины отрыва в бетонных и железобетонных образцах распространяются (с некоторым приближением) в направлении изостат I рода… Большее отклонение трещин от изостат, построенных в предположении упругой работы материала, наблюдается вблизи арматуры, что объясняется действием значительных напряжений на контакте арматуры и бетона.
Таким образом, трещина, по которым разрушаются железобетонные конструкции, в основном являются трещинами нормального отрыва. Разрушение изгибаемых конструкций по наклонным сечениям происходит при развитии трещин отрыва в сжатую зону. При небольшом расстоянии от опоры до ближайшей внешней силы трещина проходит по самой короткой изостате. Разрушение изгибаемой балки по наклонной трещине при развитии ее в сжатой зоне тем менее вероятно, чем чаще расположены внешние сосредоточенные силы. При таком их расположении или при расположенной нагрузке наклонная трещина не вызывает разрушения. В этом случае разрушение начинается при развитии близких к горизонтали трещин в сжатой зоне.
Следовательно, после образования и раскрытия трещин в растянутых зонах внешняя нагрузка воспринимается условной внутренней сжатой конструкцией, в которой усилия действуют по изостатам I рода, и растянутой арматурой. Это представление продуктивно при расчете прочности фундаментов по наклонным сечениям, а также при расчете прочности плит ростверков».
Полезная литература по теме статьи:
1. Каркасно-стержневые расчетные модели и инженерные методы расчета железобетонных конструкций. Баранова Т. Н., Залесов А.С. 2003.
2. Особенности напряженно-деформированного состояния коротких железобетонных элементов. Скачков Ю. П., Снежкина О. В., Кочеткова М. В., Корнюхин А. В. // Молодой ученый. — 2013. — №12. — С. 172-175. — URL https://moluch.ru/archive/59/8366/.
3. Силовое сопротивление и разработка метода расчета железобетонных ростверков : автореферат диссертация доктора технических наук. Пенза, 2002. — 45 с.
5. Статья о «strut-and-tie» методе, с подробным описанием и примерами;
6.
СП 20.13330.2018
10.1 Нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия следует определять по формуле:
S0 = ce ct µ Sg, (10.1)
µ — коэффициент перехода от веса снегового покрова (на горизонтальной поверхности) земли к снеговой нагрузке на покрытие, принимаемый в соответствии с 10.4 (в зависимости от схемы распределения снеговой нагрузки на покрытии и от конфигурации кровли);
Sg – нормативное значение веса снегового покрова на 1 м горизонтальной поверхности земли (на высоте не более 1500 м над уровнем моря), принимаемое в соответствии с 10.2.
Задача.
Найти пониженное значение (длительную часть) снеговой нагрузки для местности I с температурой января минус 20 град. Покрытие здание — плоское, с углом наклона менее 30 град.
Решение.
По таблице 10.1 для местности I Sg = 0,5 кПа.
µ = 1 (при уклоне покрытия менее 30 градусов).
S0 = ce ct 0,5 = 0,5 ce ct, кПа — нормативное значение снеговой нагрузки.
10.11 Для районов со средней температурой января минус 5°С и ниже (по таблице 5.1 СП 131.13330) пониженное нормативное значение снеговой нагрузки (см. 4.1) определяется умножением ее нормативного значения на коэффициент 0,5. При этом коэффициенты сe и сt принимаются равными единице.
Пониженная (длительная) часть будет равна Sпон. = S0 х 0,5 = 0,5 х 0,5 = 0,25.
P.S. Длительная часть снеговой нагрузки используется для расчета конструкций по второму предельному состоянию (например, при расчете продолжительной ширины раскрытия трещин, эстетико-психологических прогибов, осадок зданий и др.).
Ссылки: