Как известно, разрушение изгибаемых железобетонных элементов по наклонным сечениям происходит при одновременном действии поперечной силы Q и изгибающего момента М.
При опирании плит на монолитные стены, при проверке наклонных сечений, вырезают полосу плиты шириной 1 м.
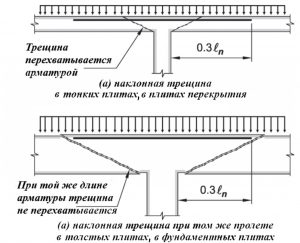
При превышении …. в бетоне образуется наклонная трещина (вызываемые главными растягивающими напряжениями), проходящая через всю зону растянутого бетона.
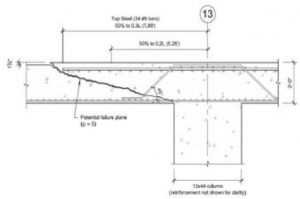
Наклонная трещина в толстых плитах при недостаточной длине верхней продольной арматуры может уходить за стержень
Процесс образования наклонной трещины
Вследствие неупругих свойств бетона касательные напряжения распределяются равномерно по сечению, поэтому наклонная трещина раскрывается примерно одинаково по всей длине. При разрушении происходит взаимное смещение частей элемента по вертикали.
По мере увеличения нагрузки, в поперечной арматуре растут напряжения, достигая расчетного сопротивления, а затем, в процессе текучести, наступает также предельное состояние либо бетона над наклонной трещиной, либо продольной арматуры. В первом случае разрушение бетона вызовет разрушение элемента в целом (от действия момента поворачиваются части элемента относительно центра тяжести сжатой зоны бетона над трещиной. При этом трещина раскрывается, развивается по высоте, сокращается сжатая зона бетона. Напряжения в бетоне достигают предельных и происходит разрушение элемента), хотя напряжения в продольной арматуре и не достигли предельных значений. Во втором случае (сечение продольной арматуры достаточно и обеспечена её надёжная анкеровка, что препятствует повороту обеих частей элемента. Разрушение по наклонному сечению происходит после достижения предельных значений в поперечной арматуре из-за среза бетона над наклонной трещиной. Обе части элемента смещаются друг относительно друга. Такое разрушение вызывается действием поперечной силой) нагрузка может расти и далее, пока не разрушится бетон над трещиной или не нарушится анкеровка продольной арматуры, находящейся под предельным напряжением. Возможен и третий вариант разрушения — при значительном насыщении элемента поперечной арматурой она не может достичь своих предельных сопротивлений и элемент разрушается от раздавливания бетона в середине высоты элемента, между наклонными трещинами (в тавровых и двутавровых элементах при малой ширине стенки). Во всех случаях исчерпание прочности элемента определяется совместным действием изгибающего и крутящего моментов, поперечной и продольной сил.
Расчет по сжатой и растянутой зонам наклонной трещины выполняют независимо один от другого. При этом для оценки прочности по сжатой зоне используют уравнения равновесия поперечных сил, а по растянутой — уравнение равновесия моментов в наклонном сечении, считая, что разрушение по сжатой зоне происходит при преимущественных деформациях сдвига, а по растянутой — при преимущественных деформациях поворота двух блоков, разделенных наклонной трещиной, один относительно другого.
В общем случае должна рассматриваться система трех уравнений равновесия в наклонном сечении — равновесия поперечных сил, равновесия моментов, равновесия продольных сил. Однако, такой методики в нормах, пока, нет, поэтому рассматривают раздельный расчет на действие поперечной силы и на действие момента в наклонном сечении. Кроме того, пока не известно, как влияют на прочность наклонного сечения величины моментов, поперечных и продольных сил, при совместном их взаимодействии…
Напряжения в продольной арматуре к моменту разрушения сечения, как правило, не достигают своих предельных значений, т.е. расчетных сопротивлений. Так как в этих стержнях достигается предел текучести по всей площади стержня, то в арматуре действуют лишь осевые усилия, а поперечные, «нагельные», являются весьма незначительными. Так как наклонные трещины имеют криволинейное очертание, то при смещении берегов трещины возникают силы зацепления выступов, находящихся на берегах трещин, кроме того поверхность бетона в наклонной трещине шероховатая, этот факт также помогает бетонным поверхностям зацепляться друг о друга.
При этом сумма проекций внешних сил на ось, нормальную к оси балки, численно равна поперечной силе в поперечном сечении, совпадающем со сжатой зоной, а момент внешних сил относительно центра сжатой зоны численно равен изгибающему моменту в том же поперечном сечении. При расчете определяют независимо друг от друга предельные величины поперечной силы и изгибающего момента. Усилия в наклонных и вертикальных элементах арматуры входят в оба уравнения; условно расчет ведут раздельно для поперечной силы и изгибающего момента, но к расчетным сопротивлениям наклонной и поперечной арматуры вводят понижающие коэффициенты условий работы.
Наклонные трещины в стенке появляются в случае исчерпания предельной растяжимости бетона. Деформации растяжения вызываются целым рядом факторов: действием главных растягивающих напряжений от внешних сил и усилий преднапряжения, неравномерной и стесненной усадкой бетона, температурными воздействиями. Кроме того, механические свойства бетона крайне неоднородны. Поэтому трудно заранее предвидеть, где появится первая трещина в бетоне. В дальнейшем вследствие концентрации напряжений у концов трещин они развиваются опять–таки в направлении наименьшего сопротивления. Таким образом, процесс возникновения и развития трещины в бетоне является случайным процессом, и хотя можно предвидеть общий характер трещинообразования, точное местоположение и угол наклона трещины предугадать невозможно.
Поэтому в расчет вводят самое опасное положение трещины, т. е. такое, при котором сопротивление наклонного сечения оказывается наименьшим. Условием этого является минимальное значение отношения Qпр/Q. Приближенно его часто заменяют условием, чтобы наименьшее возможное значение имела предельная поперечная сила Qпр.
Расчет внецентренно сжатых элементов производят так же, как для изгибаемых элементов, без учета влияния нормальной силы. Это довольно грубое упрощение идет в запас прочности, так как сжимающее усилие увеличивает сопротивление сжатой зоны бетона срезу.
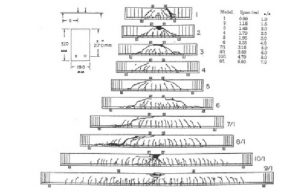
Изменение распределения трещин в зависимости от отношения высоты сечения к пролету балки (от преобладающих наклонных трещин до преобладающих нормальных трещин при большом пролете)
Расчет наклонных сечений в большей степени актуален для балок, однако, существуют методики расчета наклонных сечений и монолитных железобетонных плит перекрытий, опирающихся на колонны квадратного (и близкого к квадратному) сечения. Данная методика, в частности, подробно описана в диссертации Шеховцова И. В. «Прочность и деформативность железобетонных плит без поперечной арматуры при продавливании». Суть метода основывается на предположении, что несущая способность плиты на продавливание может быть определена, как несущая способность перекрестных балок приведенной ширины от действия поперечных сил. Рассматривается случай разрушения по сжатой зоне бетона в результате среза бетона над наклонной трещиной каждой из балок.
Бывают и смешанные расчеты на продавливание и наклонные сечения, в частности, в серии Б1.020.1-7 допускается производить расчет только примыкающих к колонне ригелей, а расчет на продавливание не производить.
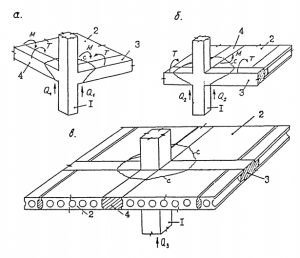
Рис.1 Различные типы примыкания ригелей к колонне. Область продавливания обозначена контуром «с». Расчет на продавливание заменяется расчетом наклонных сечений примыкающих ригелей
Ссылки: