О разных типах конечных элементов и их особенностях

В современных расчетных программах используются разные типы конечных элементов. О некоторых из них (и их особенностях) вы узнаете из этой статьи.

Изгибные элементы на основе теории толстых плит Миндлина-Рейснера. Поперечное перемещение на границе элемента аппроксимируется полиномом второго порядка, а углы поворота нормали — полиномом первого порядка. Также используется квадратичная аппроксимация напряжений по площади элемента (для четырехугольных элементов) и линейная аппроксимация напряжений по площади элемента (для треугольных элементов). Эти элементы свободны от эффекта «сдвигового запирания» и могут использоваться для расчета толстых и тонких плит. Универсальный конечный элемент, который дает очень хорошие результаты расчета поперечной силы (независимо от отношения толщины элемента к его длине) и чуть менее точные (по сравнению с элементами теории Кирхгофа) результаты расчета моментов. Используются в программах ing+, MicroFe, STARK ES, SCAD Soft (начиная с версии 7.31), NASTRAN.

Изгибные элементы на основе теории тонких плит Кирхгофа. Элементы с использованием квадратичной аппроксимации напряжений по площади элемента (для четырехугольных элементов) или линейной аппроксимации напряжений по площади элемента (для треугольных элементов) и кубической аппроксимации поперечных перемещений по границам элемента (схема Пиана). Пиан выбрал полиномы для напряжений по области элемента и перемещений по периметру элемента. Последние играют роль множителей Лагранжа для обеспечения межэлементного равновесия. Этот метод известен как гибридный метод в напряжениях (hybridstressmethod). Один из самых точных методов расчета моментов в пластинах, он дает достаточно точные результаты расчета моментов даже при грубой сетке конечных элементов, однако, значения поперечных сил менее точные чем у пластин теории Миндлина-Рейснера. Используются в программах ing+, MicroFe, STARK ES.

Элементы метода перемещений по схеме Батоша на основе теории толстых плит Миндлина-Рейсснера. Эти элементы также свободны от эффекта «сдвигового запирания» и могут использоваться для расчета толстых и тонких плит. Данные конечные элементы (в отличии от первых двух типов) при большой их толщине и мелкой сетке разбиения дают довольно точные результаты и поперечной силы и моментов. Используются в программах ing+, MicroFe, STARK ES.

Рекомендации к построению сетки конечных элементов

Приведенные ниже рекомендации, описаны в книге: «ANSYS в руках инженера. Практическое руководство. Каплун А.Б., Морозов Е.М., Олферьева. Москва 2003» и в «ПРИМЕНЕНИЕ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ В РЕШЕНИИ ЗАДАЧ ПРИКЛАДНОЙ МЕХАНИКИ. Учебно-методическое пособие для студентов технических специальностей. А. О. Шимановский, А. В. Путято. Гомель 2008».

Линейные элементы требуют более частой сетки, чем квадратичные элементы (с одним промежуточным узлом) или кубичные (с двумя промежуточными узлами).
Упорядоченная сетка (б) является более предпочтительной, чем произвольная сетка (а):
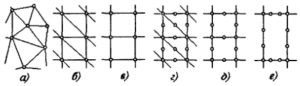
Прямоугольная сетка с 4 узлами (в) белее предпочтительна, чем сетка с треугольными элементами (б).
Сетка треугольных элементов с промежуточными узлами (г) имеет, по крайней мере, ту же самую точность, что и сетка прямоугольных элементов с 4 узлами (в).
Прямоугольная сетка с 8 узлами (д) является более предпочтительной, чем сетка треугольных элементов, с промежуточными узлами (г), несмотря на больший размер прямоугольных элементов.
Аппроксимация смещений кубическим полиномом (е) не требует более мелкой сетки.
Более частая сетка требуется там, где ожидается большой градиент деформаций или напряжений. Более редкая сетка может применяться в зонах с более или менее постоянными деформациями или напряжениями, а также в областях, не представляющих особого интереса. В связи с этим исследователь должен уметь предвидеть области концентрации напряжений:
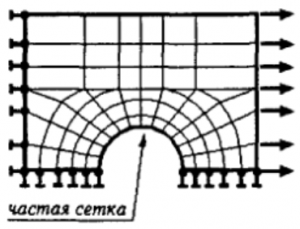
Точность результатов анализа уменьшается, если размеры соседних элементов вблизи концентратора напряжений существенно различны:
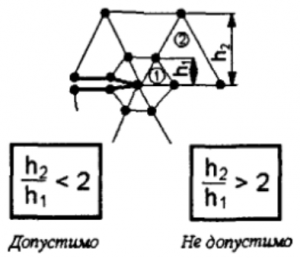
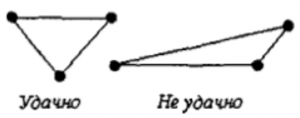
Следует избегать слишком узких и вытянутых элементов, т.к. элементы с одинаковыми, примерно, сторонами дают меньшую ошибку:
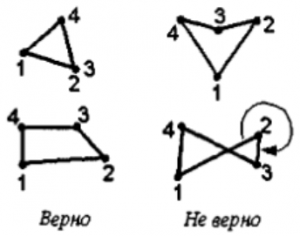
Одновременно в сетке могут присутствовать треугольные и четырехугольные элементы, однако между ними не должно быть разрывов:
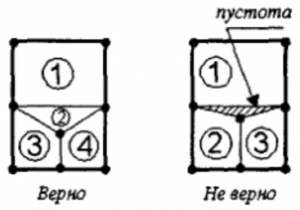
Запрещается строить четырехугольные элементы с углами более 180 градусов:

Пример моделирования пластины с наклонным вырезом (рисунок из книги «В. З. Партон. Механики разрушения от теории к практике»)

Выдержка из статьи «Методы локализации, фрагментации и техника вейвлет-анализа в применении к расчетам строительных конструкций. Золотов А.Б., Мозгалева М.Л., Медведько Д.В., Булгаков В.Е. 2008 г.»:

«основным правилом выбора шага для локально-сгущающейся сетки, справедливым и для начальных узлов, является его полное соответствие оптимальной аппроксимации производной от фундаментальной функции. В частности, для оператора Лопласа и задачи теории упругости целесообразно локальную сетку строить следующим образом: первые два шага всегда делать одинаковыми и равными шагу исходной мелкой сетки, а затем текущий шаг удваивать. Такой выбор шагов хорошо согласуется с поведением спрямления производной от фундаментальной функции. В том случае, если интересует решение в некоторой локальной зоне, в пределах этой зоны, расширенной на один шаг мелкой сетки, необходимо оставить исходный мелкий шаг, а затем увеличивать шаги по полученной формуле.»

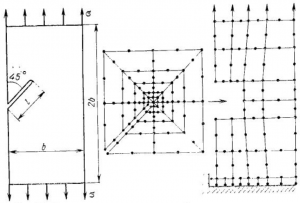
Пример построения локальной сетки в двумерном случае

Ссылки по теме данной статьи: