Прямоугольные колонны (пилоны) шириной 200 — 300 мм, в последнее время, становятся все более и более популярными. Их популярность объясняется тем, что в сочетании со стенами из блоков толщиной 200 мм, они позволяют архитекторам создавать приемлемые, для покупателей квартир, планировочные решения, с шагом колонн до 6 м. При назначении шага колонн, одним из определяющих критериев является расчета на продавливание по действующему СП 63.13330.2018. Однако, указанный в СП63 расчет не учитывает некоторые факторы, которые могут заметно снижать несущую способность плит на продавливание (без поперечной арматуры).
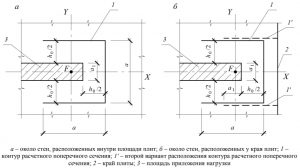
Рис. 1. Схемы расчетных контуров поперечного сечения при продавливании плоских плит из СП 430.1325800.2018
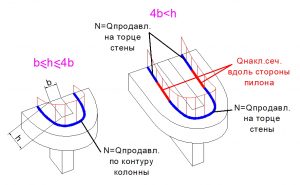
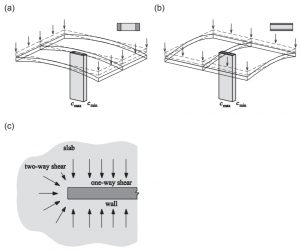
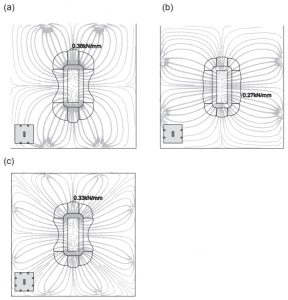
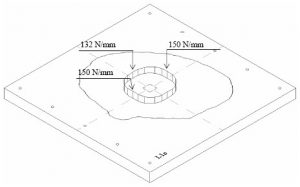
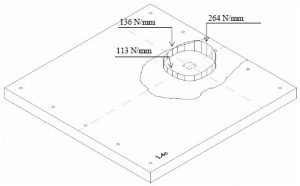
Рис. 2. Схема распределения касательных сил в плите возле крайних пилонов в зависимости от отношения длины к ширине пилона
Особенности расчета на продавливание плит перекрытий прямоугольными колоннами описаны в нормах таких стран, как США (ACI 318R-14), Бразилия (ABNT NBR 6118:2014) и Европа (EN 1992-1-1-2009), однако, в советских и российских нормах не указано никаких различий, при расчете на продавливание перекрытий средними колоннами, с соотношением сторон 1/2…1/4. В нормах лишь учитывается небольшое отличие фактического распределения напряжений в арматуре от принятой для расчета, с помощью коэффициента 0,8. В рекомендуемом (на сегодняшний день) СП 52-103-2007, в пункте 5.7, говорится о том, что колонны с соотношением сторон менее 1/4 следует относить к стенам, т.е. продавливание таких вытянутых в плане пилонов (или простенков) следует рассчитывать по двум методикам: торцевые участки рассчитывают по методике продавливания плит возле торцов стен (методика описана в «НАУЧНО-ТЕХНИЧЕСКИЙ ОТЧЕТ по теме: Разработка методики расчета и конструирования монолитных железобетонных безбалочных перекрытий, фундаментных плит и ростверков на продавливание»), а длинные стороны вытянутого пилона (простенка) рассчитывают по наклонным сечениям (по СП63). Но для пилонов с соотношением сторон 1/2…1/4 никаких специальных требований не предусмотрено, такие пилоны следует рассчитывать по той же методике, что и квадратные колонны.
На рисунках 1-5 показаны примеры возможного разрушения плит при продавливании в общем случае.
Рис. 3. Картина разрушения плиты толщиной 250 мм без поперечной арматуры при продавливании колонной сечением 130х130 мм
Рис. 4. Картина разрушения плиты толщиной 250 мм без поперечной арматуры при продавливании колонной сечением 520х520 мм
Рис. 5. Картина разрушения плиты толщиной 320 мм без поперечной арматуры при продавливании колонной сечением 340х340 мм
Рис. 6. Картина разрушения плиты толщиной 400 мм без поперечной арматуры при продавливании колонной сечением 440х440 мм
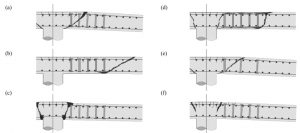
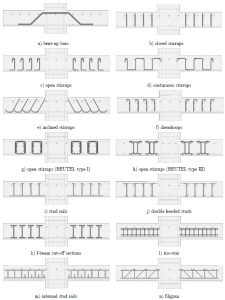
Рис. 7. Основные схемы разрушения плит с поперечной арматурой при продавливании средней колонной: а) стандартный случай по поперечной арматуре, установленной в зоне продавливания; b) разрушение за зоной установки поперечной арматуры; c) разрушение по бетону, при превышении допустимого расстояния от грани колонны до первого поперечного стержня; d) разрушение всей армированной зоны; e) разрушение по бетону меду арматурными стержнями, при превышении допустимого шага стержней; f) разрушение от разрыва продольной арматуры.
Картинки 1-5 взяты с адреса: «https://docviewer.yandex.ru/view/201669561/?*=Vw4n%2FnpBpnJmq0PMg0yraiZCgzp7InVybCI6Imh0dHBzOi8vaW5mb3NjaWVuY2UuZXBmbC5jaC9yZWNvcmQvMTgwMjIxL2ZpbGVzL0VQRkxfVEg1NDA5LnBkZiIsInRpdGxlIjoiRVBGTF9USDU0MDkucGRmIiwidWlkIjoiMjAxNjY5NTYxIiwieXUiOiIyOTM1OTQxMzcxNDUwMjEwNjQ1Iiwibm9pZnJhbWUiOnRydWUsInRzIjoxNTI4NzE3NDk5OTMyLCJzZXJwUGFyYW1zIjoibGFuZz1lbiZuYW1lPUVQRkxfVEg1NDA5LnBkZiZ0bT0xNTI4NzE2ODM4JnRsZD1ydSZ0ZXh0PUNTQ1QlMjBpcyUyMGRldmVsb3BlZCZ1cmw9aHR0cHMlM0ElMkYlMkZpbmZvc2NpZW5jZS5lcGZsLmNoJTJGcmVjb3JkJTJGMTgwMjIxJTJGZmlsZXMlMkZFUEZMX1RINTQwOS5wZGYmbHI9MjEzJm1pbWU9cGRmJmwxMG49cnUmc2lnbj1jZGM4Y2JlMzAwMzUwNzZiMGJjZDNjZmIxNDUwZTY1YyZrZXlubz0wIn0%3D&page=1&lang=en»
Рис. 8. Разные виды поперечной арматуры (Источник: «http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1679-78252016001502970»)
а) неравномерное распределение нагрузки по плите перекрытия;
в) неравные пролеты плиты (так как такие плиты, чаще всего, имеют различное продольное армирование в ортогональных направлениях, которое влияет на распределение моментов и касательных напряжений).
В другой статье бразильских исследователей
В статье «Анализ напряженно-деформированного состояния плитных конструкций в приопорных зонах. О.В. Кабанцев, К.О. Песин, А.В. Карлин. 2017», авторы, проведя численные эксперименты, приходят к следующему выводу: «…численными исследованиями установлено, что разрушение по механизму продавливания может реализоваться на краевых зонах протяженных в плане опор плит перекрытий». В статье также написано, что один из авторов был свидетелем разрушения приопорной зоны плиты перекрытия у торца протяженной в плане опоры (стены) со схемой разрушения, соответствующей механизму продавливания.
В статье «СИЛОВОЕ СОПРОТИВЛЕНИЕ ЖЕЛЕЗОБЕТОННЫХ МОНОЛИТНЫХ ПЛОСКИХ ПЛИТ ПЕРЕКРЫТИЙ ПРИ ПРОДАВЛИВАНИИ КОЛОННАМИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ. В.Б. Филатов. 2012», автор указывает на то, что модель, принятая в СП 52 (и СП 63), с равномерным распределением напряжений по периметру расчетного контура удовлетворительно соответствует опытным данным, для круглых колонн и колонн с соотношением сторон не более 2. Автор пишет следующее: «При продавливании железобетонных плит колоннами прямоугольного сечения отмечено, что область наибольших деформаций в плите расположена у коротких граней колонны, вдоль длинных граней деформации плиты уменьшаются в направлении от углов колонны к ее центру. Причем эта особенность деформирования плиты по периметру колонны отмечается на всех стадиях испытания образцов, вплоть до разрушения» и предлагает считать длину условного расчетного контура, принимая в качестве граней короткую грань колонны, а также вводит коэффициент, который: «учитывает то обстоятельство, что напряжения среза, действующие в плите вдоль длинной грани колонны, либо запаздывают относительно тех же напряжений у коротких граней, либо вовсе не успевают достигнуть предельных значений, вследствие продавливания плиты на участках, прилегающих к коротким граням колонны«.
Уменьшение несущей способности на продавливание плит с прямоугольными колоннами (при соотношении сечения 1/5) также описано в » Shear Strength of Slab-Column Connections
under Gravity and Cyclic Lateral Loading. Sunendro Aris Sutanto Himawan. 2012″. В частности указывается, что при постоянном периметре продавливания, если отношение длинной стороны к короткой увеличивается, прочность на продавливание (сдвиг) уменьшается. Этот происходит из-за концентрации напряжений вдоль короткой стороны колонны».
В исследовании «“Punching Shear Strength of Slabs with Openings and Supported on Rectangular Columns. Teng, S.; Cheong, H. K.; Kuang, K. L.; and Geng J. Z., 2004”, проведенном совместно Наньянским технологическим университетом (NTU) и Строительно-монтажным управлением «Building and Construction Authority» (BCA) — Сингапур, было испытано 20 плит, с прямоугольными колоннами и отверстиями. В выводах приведены результаты, в которых указано, что усилия в плитах сконцентрированы главным образом вокруг более коротких сторон прямоугольных колонн.
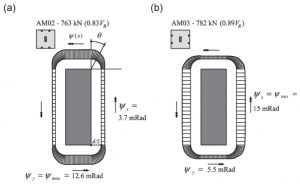
В статье: «Punching of flat slabs supported on rectangular columns” ; Engineering Structures 77 (2014) 17–33» на основании четырех экспериментом показано отличие распределения сдвиговых напряжений в зависимости от сечения колонны и от её направления относительно нагруженного пролета.
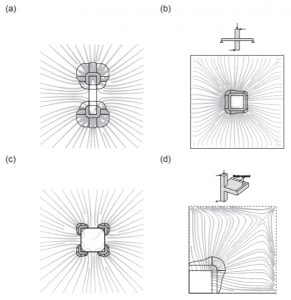
Рис. 9. Распределение касательных напряжений и трещин в плите (Источник: «http://epubs.surrey.ac.uk/805957/1/ENGSTRUCT-Punching_rectangular%20columns_FINAL%20MANUSCRIPT.pdf.pdf»)
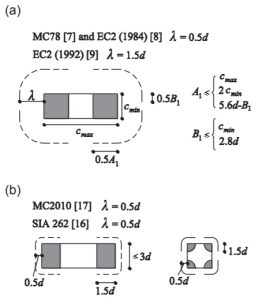
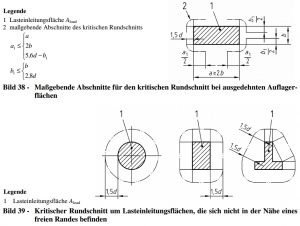
Рис. 10. Схемы определения критических зон плиты при разных типах сечений колонн (по DIN 1045-1)
Во всех перечисленных выше исследованиях и статьях общим является вывод о том, что при продавливании плит прямоугольными колоннами напряжения концентрируются вдоль коротких граней колонн (при направлении короткой стороны колонны перпендикулярно пролету плиты), что приводит к неравномерной схеме продавливания и, в результате, к снижению несущей способности плиты при данном расчете. Для квадратных колонн, при широкой стороне сечения, замечена концентрация сдвигающих напряжений на углах колонны.
Тем не менее, не смотря на большое количество экспериментальных данных, как было указано в начале данной статьи, на сегодняшний день нет полного и исчерпывающего понимания того, что и как (в какой мере) влияет на данный расчет, тем не менее, методики используемые в зарубежных нормах, в большинстве случаев, подтверждаются испытаниями и могут использоваться для проверки на продавливание плит прямоугольными колоннами.
Рис. 11. Примеры комбинированного армирования стыка плиты с колонной (Источник: «https://findpatent.ru/patent/230/2305159.html»). Использование комбинированного армирования позволяет лучше учитывать неравномерность распределения напряжений в плите в зоне ее опирании на прямоугольные пилоны с отношением сторон более 1/2. В частности, при резком повышение напряжений в плите возле узких торцов пилона (например, при неравномерном шаге колонн). Этот вариант армирования эффективен, если продавливание плиты вдоль узкого торца невозможно избежать установкой гибкой арматуры и нельзя увеличить толщину плиты или класс бетона. Примеры расчета ж/б сечений с жесткой арматурой приведены в «Руководство по проектированию железобетонных конструкций с жесткой арматурой»
В качестве примера далее приведены фрагменты текста зарубежных нормативных документов, в которых описаны особенности учета, при расчете на продавливание, прямоугольного сечения колонны.
Проверка продавливания плит прямоугольными колоннами описывается в нормах США по железобетону — ACI 318R-14, в пункте 22.6.5.2.
«R8.4.4 Расчетное значение сдвигающих напряжений в плите вокруг колонны, должно соответствовать пункту 22.6.
8.4.4.1.1 Плиты должны быть рассчитаны на действие двусторонних сдвигающих напряжений возле колонн, в местах приложения сосредоточенных нагрузок и на участках действия реактивных сил в соответствии с 22.6.4.
22.6.1.2 Нормативная прочность на сдвиг для элементов, работающих на изгиб в двух направлениях, без поперечной арматуры, определяется:
vu = vc (22.6.1.2)
22.6.5.2 vc определяется в соответствии с Таблицей 22.6.5.2.
Для обычного тяжелого бетона коэффициент лямбда принимается равной единице.
f’c — расчетная прочность бетона при сжатии (по нормам США).
R22.6.5.2 Для квадратных колонн напряжение vc ограничивается значением пункта «а» Таблицы 22.6.5.2. Однако, тесты (комитета Joint ACI-ASCE Committee 426
1974) показали, что указанное значение является небезопасным, когда отношение β длинной и короткой сторон прямоугольной колонны, или загруженной области, больше 2. В таких случаях, значение 4, в пункте «а» (вокруг углов колонны или нагруженная область) заменяется на 2. Другие испытания (Vanderbilt 1972), указывают на то, что значение vc уменьшается по мере увеличения соотношения b0/d. Выражения в пунктах (b) и (с) Таблицы 22.6.5.2 были добавлены для учета этих двух эффектов».
Проверка продавливания плит прямоугольными колоннами в Европейских нормах по железобетону — EN 1992-1-1-2009.
6.4.3 Расчет на продавливание
(2) Следует выполнить следующие проверки:
а) Вдоль периметра колонны или периметра площади приложения нагрузки максимальное напряжение от продавливания не должно быть превышено:
vEd <= vRd,max
б) Поперечная арматура из условия продавливания не требуется, если
vEd = vRd,с
с) Если значение vEd превышают vRd,c для рассматриваемого контрольного сечения, необходимо предусмотреть поперечную арматуру от продавливания согласно 6.4.5.
(3) Если реакция опоры действует с эксцентриситетом по отношению к контрольному периметру, необходимо определить максимальное напряжение по формуле:
vEd = β (VEd / ui d),
где d — средняя полезная высота плиты, принимаемая равной (dy + dz)/2;
dy, dz — полезная высота плиты в направлениях y и z соответственно в контрольном сечении;
ui — длина рассматриваемого контрольного периметра;
β — определяется по формуле:
при одноосном изгибе β = 1 + k β (MEd / VEd) (ui / Wi),
здесь ui — длина основного контрольного периметра;
k — коэффициент, зависящий от отношения размеров колонны с1 и с2: его значение является функцией пропорции неуравновешенного момента, переданного поперечной силой и совместно изгибом и кручением (таблица 6.1);
Таблица 6.1 — Значения k прямоугольных площадей приложения нагрузки
|
с1/с2 |
<=0,5 | 1,0 | 2,0 | >=3,0 |
| k | 0,45 | 0,60 | 0,70 |
0,80 |
Wi — соответствует распределению поперечного усилия, представленному на рисунке 6.19, и является функцией основного контрольного периметра ui:
dl — приращение длины периметра;
е — расстояние от dl до оси, вокруг которой действует момент MEd
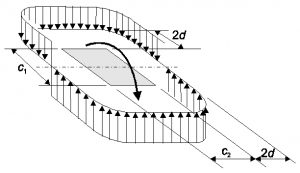
Рис. 12. — Распределение поперечного усилия при неуравновешенном моменте в узле «плита — внутренняя колонна»
В руководстве для проектировщиков к Еврокоду 2 про коэффициент β написано следующее: «При расчете силы сдвига принято считать, что такая сила распределяется равномерно по критическому периметру. В действительности это не так, в частности, в месте соединения плиты и колонны, где отмечается передача момента между плитой и колонной. Точный расчет может показать, что в таком случае распределение силы сдвига по периметру неравномерное, а сама сила сдвига сопровождается крутящими моментами. Результаты масштабных экспериментов показали, что продавливание значительно меньше там, где происходит передача моментов. Это свидетельствует о том, что продавливание — это не исключительно пластический феномен: сдвиг в предельном состоянии по несущей способности нельзя распределить по периметру полностью. Чтобы учесть эти факторы, в расчете при проектировании используется коэффициент, который является функцией геометрической формы критического периметра и прикладываемых моментов. EN 1992-1-1 предлагает использовать коэффициент β, который увеличивает среднее напряжение сдвига вокруг периметра».
Для прямоугольных колонн
где c1 — размер колонны параллельно эксцентриситету нагрузки;
c2 — размер колонны перпендикулярно эксцентриситету нагрузки.
Для внутренней прямоугольной колонны, при нагрузке, приложенной с эксцентриситетом по отношению к обеим осям, β определяется приближенно по формуле
где ey и ez — эксцентриситеты MEd/VEd, соответственно вдоль осей y и z;
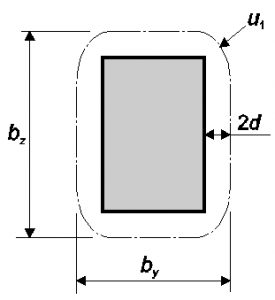
by и bz — размеры контрольного периметра (см. рисунок 7).
Рис. 13. Контрольный периметры колонны прямоугольного сечения вокруг площадей приложения нагрузки
Примечание — еу определяется из момента относительно оси z, еz — из момента относительно оси у.
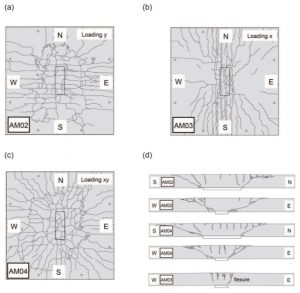
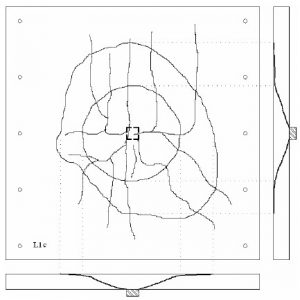
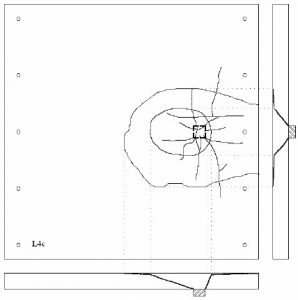
Рис. 14. Схема распределения трещин при расположении колонны в центре плиты (с равными пролетами)
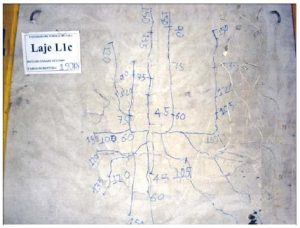
Рис. 15. Снимок трещин на плите
Рис. 16. Углы наклона трещин по X
Рис. 17. Углы наклона трещин по Y
Рис. 18. Значения напряжений в аналитической модели
Рис. 19. Схема распределения трещин при расположении колонны возле края плиты (при неравных пролетах)
Рис. 20. Снимок трещин на плите
Рис. 21. Углы наклона трещин по X
Рис. 22. Углы наклона трещин по Y
Рис. 23. Значения напряжений в аналитической модели
Эксперимент описан в статье «ANALISE EXPERIMENTAL DE LAJES LISAS UNIDIRECIONAIS DE CONCRETO ARMADO AO PUNCIONAMENTO SIMETRICO OU ASSIMETRICO. Belem 2006».
Заключение.
Анализ вышеописанной литературы позволяет сделать следующие выводы:
-
- Плиты перекрытия опирающиеся на внутренние прямоугольные колонны с отношением сторон сечения 1/1 — 1/2 необходимо считать на продавливание только по замкнутому расчетному контуру вокруг колонны;
- Плиты перекрытия опирающиеся на внутренние прямоугольные колонны с отношением сторон сечения 1/2 — 1/4 необходимо считать на продавливание по замкнутому расчетному контуру, а также выполнять проверку продавливания плиты на торцевой части колонны и проверку наклонных сечений плиты вдоль длинной стороны колонны;
- Плиты перекрытия опирающиеся на внутренние прямоугольные колонны с отношением сторон сечения более 1/4 необходимо считать на продавливание только на торцевой (узкой) части пилона, а также делать проверку плиты по наклонным сечениям вдоль длинной (широкой) стороны колонны. Считать продавливание по замкнутому расчетному контуру вокруг колонны в данном случае не следует.
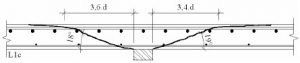
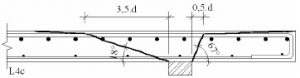
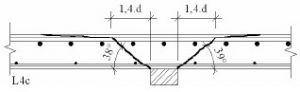
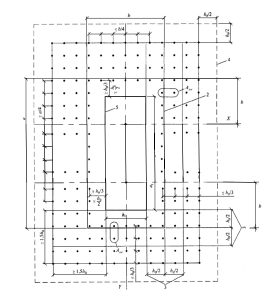 Рис. 24. Схема расположения поперечной арматуры пилона при соотношении его сторон 1/4-1/6 и величине продавливающей силы 1.3Fb,ult>Fпр>Fb,ult. При значениях продавливающей силы пилона 1.3Fb,ult<=Fпр<2Fb,ult поперечную арматуру следует устанавливать равномерно по всему контуру, включая среднюю часть пилона. В любом случае, следует отдельно проверять торцевые участки пилона, чтобы величина продавливающей силы Fпр на этих участках не превосходила 2Fb,ult. Продавливающую сила для проверки торцов принимается равной суммарной поперечной силе вдоль расчетного контура длиной 3b (см. картинку). Обозначения на картинке взяты из СП 63.13330.2012
Рис. 24. Схема расположения поперечной арматуры пилона при соотношении его сторон 1/4-1/6 и величине продавливающей силы 1.3Fb,ult>Fпр>Fb,ult. При значениях продавливающей силы пилона 1.3Fb,ult<=Fпр<2Fb,ult поперечную арматуру следует устанавливать равномерно по всему контуру, включая среднюю часть пилона. В любом случае, следует отдельно проверять торцевые участки пилона, чтобы величина продавливающей силы Fпр на этих участках не превосходила 2Fb,ult. Продавливающую сила для проверки торцов принимается равной суммарной поперечной силе вдоль расчетного контура длиной 3b (см. картинку). Обозначения на картинке взяты из СП 63.13330.2012
2. Ссылка на статью об осреднении поперечной арматуры;
4. Пример ручного расчета на сдвиг по ACI 318;
9. Расчет на продавливание с учетом формы разрушения. (Источник: «Журнал «Бетон и железобетон»»);


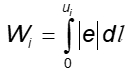
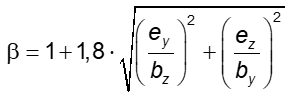


Добрый вечер.
Расчет может потребоваться для прямоугольных плит балочного типа, например, опирающихся на пилоны только по двум противоположным сторонам (при направлении пилонов параллельно длинному пролету), и с большой нагрузкой на плиту. Также может потребоваться такой расчет для тонкой фундаментной плиты при большом количестве этажей и больших пролетах перпендикулярно длинной стороне пилонов. Проверку проводят для единичной ширины сечения. Для короткой стороны выполняется проверка на продавливание, описанная в СП 430. Особенно актуально это для плит без поперечной арматуры, в которых расчет на продавливание (без поперечной арматуры) по трехстороннему (или четырехстороннему) контуру проходит, но с небольшим запасом, а максимальная концентрация поперечных усилий сосредоточена вдоль одной из длинных сторон, т.е. распределение поперечных сил неравномерное и поперечная арматура отсутствует.
Добрый день! Хочу уточнить насчет необходимости «делать проверку плиты по наклонным сечениям вдоль длинной (широкой) стороны колонны»: в таком случае плита считается по наклонным сечениям как балка с шириной, равной длине пилона?
Насколько действительно необходима эта проверка для плит? В плитах ведь касательные напряжения распределяются иначе по сравнению по стержневыми элементами и обычно плиты на Q не считают